Hallo,
Ein Gleichungssystem mit den 2 Unbekannten \(x\) und \(y\) kann allgemein z.B. so aussehen $$\begin{aligned} ax + by &= c \\ dx + ey &= f\end{aligned}$$Nehmen wir ganz konkret mal das Gleichungssystem$$\begin{aligned} 3x + y &= 14 \\ -2x + 3y &= 9\end{aligned}$$Jede Gleichung für sich genommen, hat i.A. unendlich viele Lösung. Wenn Du z.B. in der ersten Gleichung für \(x=2\) setzt, dann ist mit \(y=8\) die Gleichung erfüllt. \((2;8)\) ist hier eine Lösung für die Gleichung \(3x + y = 14\). Dies kann man auch als Punkt in ein Koordinatensytem eintragen. Genau wie das Paar \((4;2)\). Dies sind die Punkte \(P_1\) und \(P_2\) in folgender Skizze:
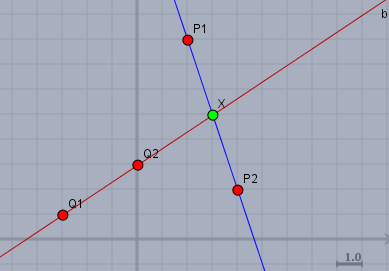
Wenn Du dies nun für alle möglichen Lösungen machst, so erhältst Du die blaue Gerade. Das kann man genauso für die zweite Gleichung machen. Hier sind z.B. \(Q_1=(-3;1)\) und \(Q_2=(0;3)\) Lösungen für die Gleichung \(-2x + 3y = 9\). Würde man alle Lösungen der zweiten Gleichung in das Koordinatenkreuz einzeichnen, so erhält man die rote Gerade.
Damit kann also ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten als ein Geradenpaar in einem Koordinatensystem aufgefasst werden. Und wenn sich die Geraden schneiden, so ist der Schnittpunkt die Lösung des Gleichungssystem. Hier erfüllt \(X=(3;5)\) beide(!) Gleichungen.