Wie rechne ich bei diesem Dreieck den Flächeninhalt und die Höhe?

Question

Gegeben ist ein Dreieck mit den Seiten a= 45 mm; b= 36 mm und der Höhe h_a = 20mm
Berechnen Sie den Flächeninhalt und die Höhe h_b des Dreiecks.

Danke im Vorhinein!

Answer 1

Hi

A = (a*h_a)/2

A = \( \frac{45*20}{2} \)

A = 450 mm²

Aus dem Flächeninhalt kann man die Höhe h_b ermitteln.

Es gilt: A = (a*h_a)/2 = (b*h_b)/2 = ( c*h_c)/2

A = (b*h_b)/2

450 =    (36*h_b)/2                I *2

900 = 36 h_b                        I :36

 h_b = 25 mm

Answer 2

Hallo Berni,

die Fläche eines Dreiecks ist doch Grundseite mal Höhe durch 2. Und was Grundseite und Höhe ist, darfst Du Dir aussuchen, es mus nur die Höhe senkrecht auf der Grundseite stehen. Sei \(a\) die Grundseite, dann ist die Fläche \(F\)$$F = \frac 12 ah_a = \frac 12 \cdot 45 \text{mm} \cdot 20\text{mm} = 450 \text{mm}^2 = 4,5 \text{cm}^2$$Dann nimm \(b\) als Grundseite$$F = \frac 12 bh_b \implies h_b = \frac{2F}{b} = \frac{2 \cdot 450 \text{mm}^2}{36 \text{mm}} = 25\text{mm}$$Prüfe das ganze nach, indem Du das Dreieck konstruierst

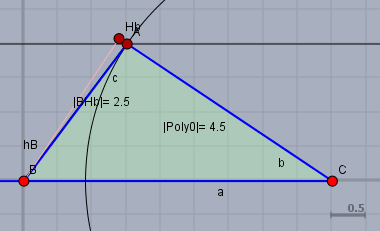
ist ein wenig tricky, da die Punkt \(A\) und \(H_b\) dicht bei einander liegen. Aber wie erwartet ist \(h_b=2,5\text{cm}\).

Gruß Werner