Wie berechnet man die Zahlenpaare?

Question

1) Uberprufe durch Einsetzen, ob die Zahlenpaare Losungen der Gleichung sind
    a) 2x=3y+6    (-1;-3); (4,8 ; 1,2);  (3;0)
    b) 7x-5y=9    (1;2)    (2;1)  (-3;-6)
2) Gib yeweils funf Zahlenpaare an, die losungen der Fleichung sind!
    a) 12x+2y=0
    b) 2y-4x=18
3) Forme die Gleichungen nach den Variablen x oder y um! Wahle dabei die
Gunstige Variante! Gib anschliessend drei Zahlenpaare an, die Losungsmenge der Gleichung gehoren!
   a) X+y=16
   b) 5x-2,5y=120

4)   Stelle die Gleichungen nach der Variable y um und zeichne den zugehorigen Graphen!
            a) Y=2x-1
            b) Y=-x-2,5

Answer 1

a) 2x=3y+6    (-1;-3);

Du setzt für x -1 und für y -3 ein:

$$2\cdot(-1)=3\cdot(-3)+6\\-2=-3$$

Der Punkt liegt also nicht auf der Geraden

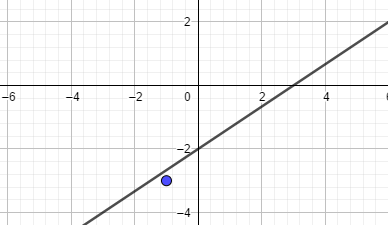
 Bei den anderen Aufgaben gehst du ebenso vor.

2) Gib jeweils fünf Zahlenpaare an, die Lösungen der Gleichung sind!
    a) 12x+2y=0

$$12x+2y=0\\y=-12x $$

Entweder zeichnest du die Gerade ein und liest Zahlenpaare ab, oder du gibst für x beliebige Zahlen ein und berechnest y.

3) Forme die Gleichungen nach den Variablen x oder y um! Wähle dabei die
günstige Variante! Gib anschliessend drei Zahlenpaare an, die zur Lösungsmenge der Gleichung gehören!
  a) X+y=16
  b) 5x-2,5y=120

Das solltest du alleine schaffen.

4)  Stelle die Gleichungen nach der Variable y um und zeichne den zugehorigen Graphen!
            a) Y=2x-1
            b) Y=-x-2,5

Umgestellt sind die Gleichungen schon, zum Zeichnen würde ich so vorgehen.

y = mx + b

Schnittpunkt mit der y-Achse markieren, den du aus der Gleichung ablesen kannst. Anschließend eine Einheit nach rechts und dann m Einheiten nach oben, wenn m > 0 bzw. m Einheiten nach unten, wenn m < 0. Dann die beiden Punkte miteinander verbinden.

Comments

2)  2y-4x=18   x=1

     2y-4*1=18 |-4

    2y=14 | 2

    y=  7

Ist dass richtig?

---

Du rechnest auf beiden Seiten +4 und teilst dann durch 2 ⇒ y = 11

---

Ist dass richtig?

Fast, in der 2. Zeile hast du einen Fehler gemacht. Du hast:

2y-4=18

Damit die 4 auf der linken Seite "weggeht", musst du +4 rechnen, nicht -4.

2y-4(+4)=18(+4)

2y=22

y=11

Man kann seine Ergebnisse auch immer überprüfen, indem man x und y in die ursprüngliche Gleichung einsetzt:

2*(7)-4=10≠18

2*(11)-4=22-4=18 \(\checkmark\)

---

kannst du mir helfen mit nummer 3?

---

x + y = 16

y = 16 - x

x = 1 ⇒ y = 15

usw.

5x - 2,5y = 120

-2,5y = 120 - 5x

y = 2x -48

x = 24 ⇒ y = 0

usw.

---

wie hasst du das ausgerechnet? y = 2x -48

---

$$5x-2,5y=120\quad |-5x\\-2,5y = 120 - 5x\quad |: (-2,5)\\ y = -48 + 2x\\y=2x-48$$

---

Ich habe falsch geschrieben beim 4 aufgabe

c) 2x+3=6

ich rechne es so:

2x+3 =6 | -2x

3y=6-2x | :(3)

y=2-0.6x ist das richtig?

---

Kann es ein, dass ein y in der Gleichung fehlt?

---

ja muss sein  2x+3y=6

---

Bis hierhin ist es richtig:

3y=6-2x | :(3)

Du musst dann ALLES durch 3 teilen,

also 3y : 3, 6 : 3, -2 : 3

Dann ergibt sich

y = 2 - \( \frac{2}{3} \) x

---

soll die graphe so aussehen????

---

Ja, sehr gut, so sieht er aus.

Answer 2

1.a) Schreibe Klammern statt x oder y: 2(  )=3(  )+6. Setze die erste Komponente für x und die zweite für y: Beispiel (-1;-3): 2(-1)=3(-3)+6. Rechne -2=-9+6. Vergleiche -2≠-3. Punkt liegt nicht auf der Geraden.

2.a) 12x+2y=0. Fülle die Tabelle aus:

x	0	1	2	3	5
y

Beispiel x=0: 12·0+2y=0, also y=0.

Comments

kannst du mir helfen mit nummer 3?

Answer 3

a) x+y=16 → y=16-x

    x=0 → y=16

    x=8 → y=8

   x=16 → y=0

  b) 5x-2,5y=120    |·2

      10x-5y=240      | +5y

      10x = 240+5y   |:10

         x = 24 + 0,5y

         Für y gerade Zahlen einsetzen ...

       Oder

         2x = 48+y

           y= 2x-48