Kreis an zwei anderen Kreisen konstruieren

Question

Ist es möglich, einen kreis zu konstruieren, wenn man nur 2 andere Kreise gegeben hat, die in einem größeren Kreis sind (siehe Bild)?? Der Kreis soll die 3 Kreislinien wirklich nur berühren!!

Bitte mit Konstruktionsplan!

Comments

Bitte beantworten!!! Wenn es Unklarheiten bei der Fragestellung gibt, gerne nachfragen!

---

Hast du die Mittelpunkte der beiden Kreise? Sind ihre Radien verschieden?

---

Die beiden Kreise sind gleichgroß, die bis jetzt schon vorhanden sind. Die Mittelpunkte der Kreise könnte man ja auch durch Konstruieren herausfinden: Die Mittelpunkte der beiden Kreise liegen beide auf dem Durchmesser des größten Kreises.

---

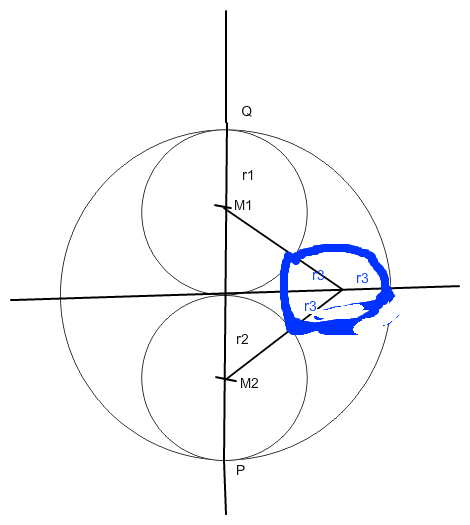
Falls da alle 3 Kreise gegeben sind und du noch eine vierten konstruieren sollst, hatte ich deine Frage nicht verstanden. Ich dachte du suchst den grossen Kreis.

Nun: Ein zusätzlicher müsste M auf der Mittelsenkrechten von P und Q haben. Weiter komme ich dann allerdings nicht sofort. Könnte es sein, dass die 3 Berührpunkte ein gleichseitiges Dreieck bilden?

(r1 + r3)^2 = r1^2 + (2r1 - r3)^2

Löse die Formel aus dem Pythagoras mal nach r3 auf.

---

da kommt raus 6r3= 4r1

---

Das wäre dann r3 = 2/3 r1.

Die Strecke r1 kannst du z.B.  mit Hilfe des Strahlensatzes dritteln.

Und dann das Resultat 2 mal zu r1 addieren und einen Hilfskreis mit Radius r1 + 2/3 r1 um M1 mit der Mittelsenkrechten schneiden. Sollte nun M3 sein.

Answer 1

Hier der Beschrieb der Konstruktion:

Eigentlich musst du eine Gerade durch die beiden Mittelpunkte zeichnen.

Diese Gerade mit den beiden Kreisen schneiden.

Die Punkte aussen P und Q nennen.
Die Mittelsenkrechte m von |PQ| konstruieren.

m mit (PQ) schneiden. Das ist nun der Mittelpunkt des gesuchten Kreises. Sein Radius ist r1 + r2 = |PQ| / 2.

Er geht durch P und Q.

Comments

"[...] Diese Gerade mit den beiden Kreisen schneiden. Die Punkte außen P und Q nennen. [...]"

Wie meinst du das? Wenn man eine Gerade konstruiert, die durch die beiden Mittelpunkte geht (Durchmesser von größtem Kreis) dann sehe ich da keine "Punkte außen". Was meinst du damit?

---

Hier mal P und Q in deiner Skizze ergänzt: