Lineare Funktion f(x): y = -x + 5 und g(x) mit Nullstelle x0=-4 und Anstieg m=2...

Question

Gegeben sind \( \mathrm{zwei} \) lineare Funktionen mit \( \mathrm{x} \in \mathbf{R} \):

\( f(x) \) mit der Gleichung \( y=-x+5 \) und \( \mathrm{g}(\mathrm{x}) \mathrm{mit} \) der Nullstelle \( \mathrm{x}_{0}=-4 \) und dem Anstieg \( \mathrm{m}=2 \).

a) Stellen Sie diese Funktionen in ein und demselben Koordinatensystem dar. Die Gleichungen der beiden Funktionen \( f(x) \) und \( g(x) \) bilden ein Gleichungssystem.

b) Geben Sie die Lösung dieses Gleichungssystems an.

Answer 1

Hi,

von g(x) solltest Du sofort erkennen, dass die allgemeine Form einer Gerade mit y = mx+b m zu 2 bestimmt werden kann. Nun noch die Nullstelle N(-4|0) eingesetzt:

0 = 2*(-4)+b

b = 8

--> g(x) = 2x+8

 

Das Schaubild also:

 

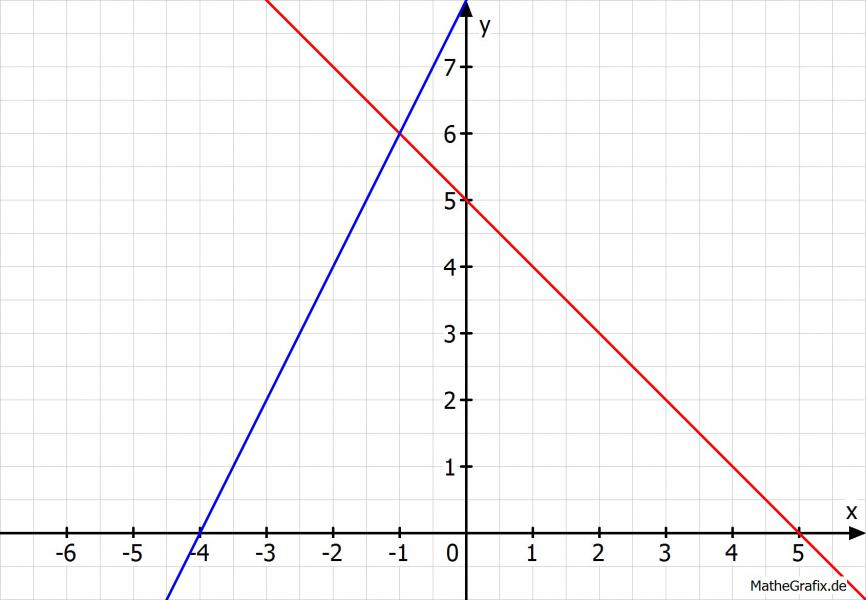
Da von "Angeben" die Rede ist und wir ja gerade das Schaubild gezeichnet haben, ist ein Ablesen sicher erlaubt:

Schnittpunkt liegt bei S(-1|6) (also x = -1 und y = 6 löst das Gleichungssystem).

Zur Übung kannst Du es ja auch noch durch Rechnung bestätigen ;).

 

Grüße

Answer 2

a)

lineare Funktion f(x) mit Gleichung y = -x + 5 und

g(x) mit Nullstelle x0=-4 und Anstieg m=2.

Ansatz m einsetzen

g(x): y = 2x + q

Nullstelle

0 = 2*(-4) + q ==> q = 8

y = 2x + 8


b) LGS

 y = -x + 5

y = 2x + 8

Gleichsetzen

-x + 5 = 2x + 8

-3 = 3x

-1 = x

Einsetzen in eine der Gleichungen y = -(-1) + 5 = 6

Schnittpunkt S(-1, 6)

L = {(-1,6)} d.h. x = -1 und y = 6.

Kontrolle in der Zeichnung.