Geben Sie eine 2 Parameterdarstellung von g an

Question

ich besuche momentan die Q1 und komme bei diesem Thema bzw. Dem folgenden Aufgabenformat einfach nicht weiter. Ich würde mich über eine Hilfe sehr freuen.

Aufgabe)

Eine Gerade g ist gegeben durch g:x(Pfeil über dem x)=(-5 , 3 , 1 ) untereinander+ k•(2, 1, -4) untereinander

a) Geben Sie eine zweite Parameterdarstellung von g an.

Die Frage die ich mir stelle ist, wie man die Aufgabe a löst.

Vielen Dank für jegliche Hilfe.

Answer 1

Du suchst Dir einen anderen Punkt der ebenfalls auf der Geraden liegt. Wenn Du dann noch willst, kannst Du auch den Richtungsvektor noch strecken oder stauchen.

Comments

Erst einmal Kann ich einen willkürlichen Punkt wählen wie z.B. P(3, 2, 5)als Bsp , oder wie macht man das? Den Richtungsvektor streckt man doch mit•2 oder nicht. Das Problem ist, dass wir dieses Thema uns selbst beibringen müssen durch Corona und deswegen die Grundlage fehlt.

Vielen Dank für die Antwort.

Answer 2

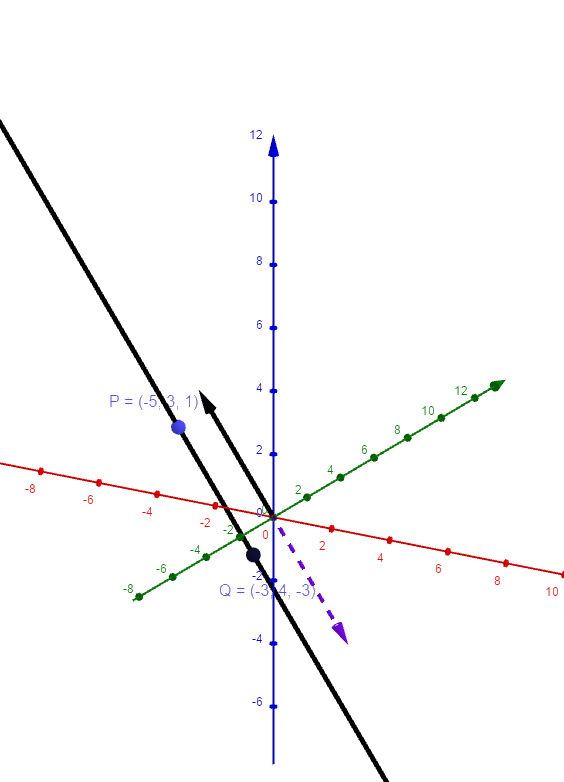
Hallo,

durch die Geradengleichung

$$g:\vec{x}=\begin{pmatrix} -5\\3\\1 \end{pmatrix}+k\cdot\begin{pmatrix} 2\\1\\-4 \end{pmatrix}$$

siehst du

den Anbindungspunkt/Stützvektor P \( \begin{pmatrix} -5\\3\\1 \end{pmatrix} \) der Geraden und ihren Richtungsvektor  \( \begin{pmatrix} 2\\1\\-4 \end{pmatrix} \) (lila)

Du kannst für k z.B. -1 einsetzen und den Richtungsvektor damit multiplizieren: \( \begin{pmatrix} -2\\-1\\4 \end{pmatrix} \) (schwarz).

Dann wäre eine weitere Geradengleichung:

$$g:\vec{x}=\begin{pmatrix} -5\\3\\1 \end{pmatrix}+k\cdot\begin{pmatrix} -2\\-1\\4 \end{pmatrix}$$

Einen weiteren Punkt auf der Geraden erhältst du, wenn du zum Ortsvektor den Richtungsvektor (oder ein Vielfaches, ein Teil von ihm) addierst:

$$\begin{pmatrix} -5+2\\3+1\\1-4 \end{pmatrix}=\begin{pmatrix} -3\\4\\-3 \end{pmatrix}$$

Dann wäre eine weitere Form der Gleichung mit gleichem Richtungsvektor:

$$g:\vec{x}=\begin{pmatrix} -3\\4\\-3 \end{pmatrix}+k\cdot\begin{pmatrix} 2\\1\\-4 \end{pmatrix}$$