Wie berechne ich die Kraft der beiden Seilen

Question

Text erkannt:

\( \theta \quad \nabla \oslash \Delta \diamond \phi \otimes \quad q \quad+ \)
\( 12 \quad F_{1} \cdot 80 N \quad \alpha_{1}=70^{\circ} \quad \alpha_{1}=40^{\circ} \quad \beta=70^{\circ} \)
\( y_{i d} \)
a) \( F_{2}=120 \mathrm{N} \quad \mathrm{s}_{14} \mathrm{s}_{2}=? \)
7
\( \alpha \)
2
2500
5
\( \uparrow P_{y}: S_{1} \cdot \sin \left(\alpha_{1}\right)=S_{2} \quad \sin \left(\alpha_{2}\right)-F_{1}-F_{2} \cdot \cos (\beta) \)
\( \frac{S_{i} \sin \left(\alpha_{1}\right)+F_{1}+F_{2} \cdot \cos (\beta)}{\sin \left(\alpha_{1}\right)} \quad s_{2}=\frac{-F_{2}-\Gamma_{2} \cos (\beta)+S_{3} \sin \left(\alpha_{1}\right)}{\sin \left(g_{1}\right)} \)
\( -r_{x}, F_{2} \cdot \sin (\beta)-s_{2}: \cos \left(\alpha_{n}\right)-s_{1} \cdot \cos \left(\alpha_{2}\right) \)
\( =\frac{F_{2} \sin (\beta)-S_{2} \cos \left(\alpha_{1}\right)}{\cos \left(\alpha_{1}\right)} \)
\( \frac{F_{2} \cdot \sin (\beta)-S_{2} \cos \left(\alpha_{2}\right)}{\cos \left(\alpha_{1}\right)}=\frac{S_{2} \sin \left(\alpha_{2}\right)+F_{1}+F_{2} \cos (\beta)}{\sin \left(\alpha_{1}\right)} \)
\( \left(F_{2} \sin (\beta)-S_{2} \cos \left(\alpha_{2}\right)\right) \cdot \sin \left(\alpha_{1}\right)=\left(S_{2} \sin \left(\alpha_{2}\right)+F_{1}+F_{2} \cdot \cos (\beta)\right): \cos \left(\alpha_{1}\right) \)
\( F_{2} \cdot \sin (\beta) \cdot \sin \left(\alpha_{1}\right)-S_{2} \cdot \cos \left(\alpha_{2}\right) \cdot \sin \left(\alpha_{1}\right)=S_{2} \sin \left(\alpha_{2}\right) \cdot \cos \left(\alpha_{2}\right)+F_{1} \cdot \cos \left(\alpha_{2}\right) \)
\( F_{2} \cos (\beta): \cos \left(\alpha_{2}\right. \)
\( F_{1} \cdot \cos \left(x_{1}\right)=F_{2} \cos (\beta) \cdot \cos \left(\alpha_{1}\right)+F_{2} \sin \beta | \sin \left(\alpha_{1}\right)=S_{2} \cdot \cos \left(\alpha_{2}\right) \cdot \sin \left(\alpha_{1}\right) \)
\( S_{2} \sin \left(\alpha_{2}\right] \cdot \cos \left(\alpha_{1}\right. \)

Text erkannt:

5 \( \nabla \oslash \Delta \otimes \phi \otimes \quad q \)
\( \left(x^{11}\right)^{2} \cdot F_{2}=120 N \quad S_{11} s_{2}=? \)
\( r \)
\( \alpha \)
2
\( x \)
set \( \underbrace{s_{2}}_{\beta} \)
\( \uparrow P_{y}: S_{1} \cdot \sin \left(\alpha_{1}\right)=S_{2} \cdot \sin \left(\alpha_{2}\right)-F_{1}-F_{2} \cdot \cos (\beta) \)
\( S=\frac{S_{i} \sin \left(\alpha_{1}\right)+F_{1}+F_{2} \cdot \cos (\beta)}{\sin \left(\alpha_{1}\right)} \cdot s_{2}=\frac{-F_{2}-\Gamma_{2} \cos (\beta)+S_{1} \sin \left(\alpha_{1}\right)}{\sin \left(g_{1}\right)} \)
\( -P_{x} \cdot F_{2} \cdot \sin (\beta)-S_{2} \cdot \cos \left(\alpha_{1}\right)-S_{1} \cdot \cos \left(\alpha_{2}\right) \)
\( s_{1}=\frac{F_{2} \sin (\beta)-\zeta_{2} \cos \left(\alpha_{1}\right)}{\cos \left(\alpha_{1} l\right.} \)
\( \frac{F_{2} \cdot \sin (\beta)-S_{2} \cos \left(\alpha_{2}\right)}{\cos \left(\alpha_{1}\right)}=\frac{S_{2} \sin \left(\alpha_{2}\right)+F_{1}+F_{2} \cos (\beta)}{\sin \left(\alpha_{1}\right)} \)
\( \left(F_{2} \sin (\beta)-S_{2} \cos \left(\alpha_{2}\right)\right) \cdot \sin \left(\alpha_{1}\right)=\left(S_{2} \sin \left(\alpha_{2}\right)+F_{1}+F_{2} \cdot \cos (\beta)\right): \cos \left(\alpha_{1}\right) \)
\( F_{2} \cdot \sin (\beta) \cdot \sin \left(\alpha_{n}\right)-S_{2} \cos \left(\alpha_{2}\right) \cdot \sin \left(\alpha_{1}\right)=S_{2} \sin \left(\alpha_{2}\right) \cdot \cos \left(\alpha_{2}\right)+F_{n} \cdot \cos \left(\alpha_{2}\right) \)
\( F_{2} \cos (\beta): \cos \left(\alpha_{2}\right. \)
\( F_{1} \cdot \cos \left(\alpha_{1}\right)-F_{2} \cos (\beta) \cdot \cos \left(\alpha_{1}\right)+F_{2} \sin (\beta) \sin \left(\alpha_{1}\right)=S_{2} \cdot \cos \left(\alpha_{1}\right) \cdot \sin \left(\alpha_{1}\right) \)
\( S_{2} \sin \left(\alpha_{2}\right] \cdot \cos \left(\alpha_{1}\right) \)
\( \approx 46 N \& \)
Rettrape Egessis \( 68 \mathrm{N} \)

Ich glaube ich habe bei diesem Problem den richtigen Ansatz gefunden. Dennoch weiß ich nicht wie ich die letzten Schritte ausführen sollte, ich glaube nämlich dass ich so zu einem falschen Ergebnis kommen. Könnte mir jemand vielleicht helfen und sagen ob ich richtig gerechnet habe beziehungsweise wo meine Fehler sind

Answer 1

Hallo,

Ich gehe mal davon aus, dass in der Zeichnung \(\alpha_1\) und \(\alpha_2\) vertauscht worden sind. Ansonsten wäre eine der Seilkräfte eine Druckkraft und Deine Rechnung wäre bereits in der ersten Zeile falsch.

Deine Rechnung kann man nicht nachvollziehen. Da müsstest Du bei der automatischen Texterkennung noch tüchtig aufräumen. ;-)

Wenn Du wissen möchtest, ob das Ergebnis richtig ist, dann schaue Dir die Zeichnung an. Die Kraft \(F_2\) ist mit \(120 \text N\) angegeben und die Resultierende ist sicher noch größer. Weiter zeigt die Resultierende in etwa in Richtung von Seil 1. D.h. die Seilkraft \(S_1\) ist in etwa so groß wie die Resultierend. Wenn man das aufzeichnet (was schneller geht als nachrechnen!) und genau nachmisst, kommt man ...

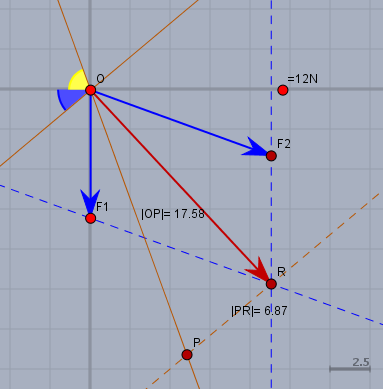
... auf \(S_1 \approx 175,8 \text N\) und \(S_2 \approx 68,7 \text N\).

Gruß Werner