Wärmeleitungsgleichung. Welche Typen für Randbedingungen wurden gewählt?

Question

Wir sehen hier die (numerische) Losung der Warmeleltungsgleichung \( u_{t}=c^{2} \Delta u \). Welche Typen für Randbedingungen wurden gewahlt?

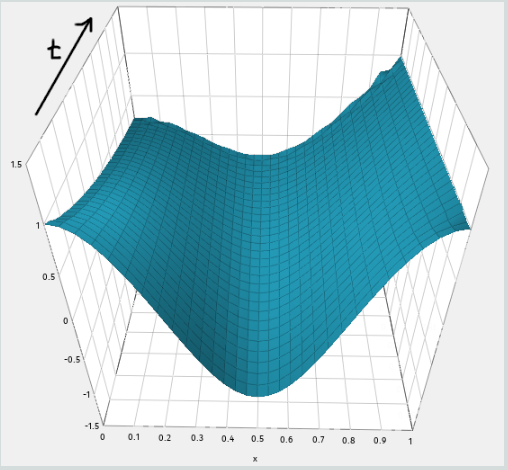
[] Dirichlet-Randbedingungen bei x=0 und bei x=1
[] Neumann-Randbedingungen bei x=0 und bei x=1
[x] Dirichlet-Randbedingungen bei x=0 und Neumann-Randbedingungen bei x=1
[] Neumann-Randbedingungen bei x=0 und Dirichlet-Randbedingungen bei x=1

In der Lösung der Wärmeleitungsgleichung war c=0,25. Was passiert, wenn c kleiner gewählt wird, z.B. c=0,05?

[x] Die zeitliche Veränderung erfolgt viel langsamer.
[] Die zeitliche Veränderung erfolgt viel schneller.
[] Es ergibt sich genau die gleiche Lösung.
[] Das Problem ist nicht mehr lösbar.

Sind hier meine Lösungen richtig so?
Gruß

Answer 1

Hallo,

ich denke, bei \( x = 1 \) wird der Wert von \( x \) festgehalten, während er bei \( x = 0 \) nicht konstant verläuft. Wie kann man von diesem Ausgangspunkt auf die plausible Lösung schließen?

Im zweiten Fall kann man diskutieren: Was gilt für die zeitliche Änderung \( u_t \) wenn man \( c \) kleiner oder größer wählt?

Grüße

Mister

Comments

dann ist das: Neumann-Randbedingungen bei x=0 und bei x=1

und wie ist die zeitliche Änderung ? ich würde sagen, dass die zeitliche Veränderung trozdem viel langsamer. erfolgt  ?

Gruß

---

Ich denke, du kommst bei der Aufgabe insgesamt weiter, wenn du deine Schlussfolgerungen gut begründen kannst.

---

je kleiner c desto kleiner u_{t....!!  damit sollte die zeit viel langsamer laufen???}

_Gruß

---

Die Zeit verläuft gleich schnell, aber der Prozess verläuft langsamer.

Hast du auch schon eine Begründung für die beidseitigen Neumann-Bedingungen?

---

Also  Neumann-Randbedingungen bei x=0 und bei x=1 ist ja richtig und damit Die zeitliche Veränderung  viel langsamer erfolgt auch richtig.

Wollen sie jetzt wissen warum die zeitliche Änderung viel langsamer erfolg?

---

Wie begründet man, dass die Neumann-Bedingungen beidseitig sind?

Oder vielleicht grundsätzlicher gefragt: Was sind Neumann-Bedingungen?

---

der Richtige Antwort müsste das hier sein. Neumann-Randbedingungen bei x=0 und Dirichlet-Randbedingungen bei x=1

Gruß

---

Sehr gut! Spät, aber richtig.

Weißt du auch, warum das die richtige Antwort ist?