Quadratische Lösung umformen

Question

0=0,25x^2+x-3..das ist die Lösung, muss graphisch zeichnen. Wie finde ich x punkte raus.

Answer 1

Hallo fatos,

Du kannst sie graphisch wie folgt lösen:

Kennst Du den Höhensatz im rechtwinkligen Dreieck? Der besagt, dass das Produkt der Hypotenusenabschnitte gleich dem Quadrat der Höhe ist. Dazu multipliziere ich die Gleichung mit 4 - damit wir gefälligere Zahlen bekommen - setzte die 12 auf die andere Seite und klammere \(x\) aus $$\begin{aligned} 0 &= 0,25 x^2 + x - 3 && \left|\, \cdot 4 \right. \\ 0&= x^2 + 4x  -12 &&\left|\,+12 \right. \\ 12 &= (x+4)x \\ h^2 &= p \cdot q && \text{Höhensatz}\end{aligned}$$

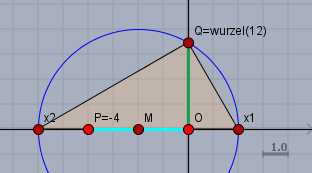
Oben die hellblaue Strecke \(PO\) hat die Länge \(4\) und die grüne senkrechte Strecke \(OQ\) die Länge \(\sqrt{12}\). Schlägt man um den Mittelpunkt \(M\) von \(PO\) einen Kreis mit Radius \(MQ\), so erhält man auf der X-Achse die Schnittpunkte \(X_1\) und \(X_2\). Die rechte Strecke \(X_2O = x + 4\) und die linke ist \(OX_1=x\) und das Produkt von beiden ist lt. Höhensatz \((x+4)x=|OQ|^2=12\).

Folglich sind \(X_1=2\) und \(X_2=-6\) die Lösungen der quadratischen Gleichung.

Gruß Werner

Answer 2

Die Gleichung lässt sich umformen zu

        x² = -4x + 12.

Zeichne die Parabel f(x) = x².

Zeichne die Gerade g(x) = -4x + 12.

Lösungen der Gleichung sind die x-Koordinaten der Schnittpunkte.

Answer 3

Die Zeichnest die Parabel mit der Gleichung f(x)=0,25x²+x-3:

und liest die Nullstellen ab. x=2 und x=-6

Comments

Danke für die Antwort