Die Geschichte der Mathematik zeigt hier schön, dass man diese Aufgabe auf zig Wegen berechnen kann.
Leider kenne ich nicht den Aufgabensteller (Klassenstufe), wofür er Punkte vergibt und welche er kennt
(viele Mathe-Lehrer kennen die PQRST-Formel nicht).
- Bisektion (siehe Wikipedia)
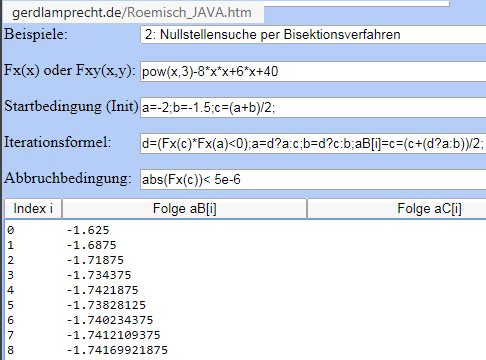
- Newton-Verfahren (siehe Wikipedia)
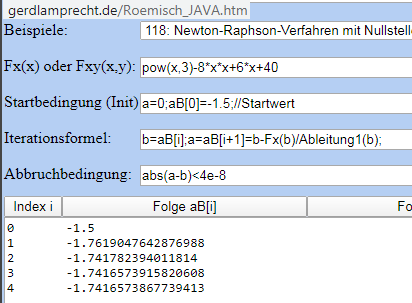
- Umstellung:
x^4-8·x^3+6·x^2+40·x = x*(x^3 - 8 x^2 + 6 x + 40)
a) Nullstellen raten -> Polynomdivision
=x*(x - 4) (x^2 - 4 x - 10) -> pq-Formel
x = 2 - sqrt(14) = -1.74165738677394138558374873232...
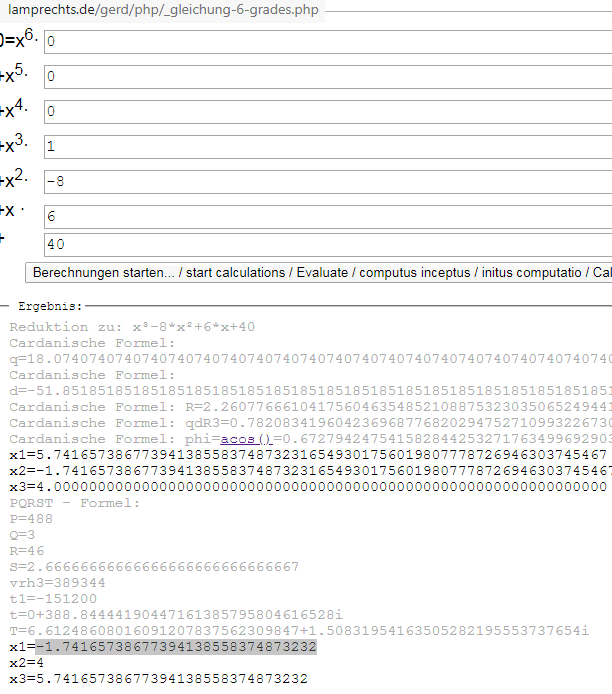
b) gleich die Cardanische Formeln oder die direkte explizite PQRST-Formel für x^3 - 8 x^2 + 6 x + 40
https://www.lamprechts.de/gerd/php/gleichung-6-grades.php
![QuadratischeGleichung_p-q-Formel_KubischeGleichung_PQRST-Formel[1].png](https://www.mathelounge.de/?qa=blob&qa_blobid=1288531336388674705)
Zugabe:
Warum nur 2 Stellen, wo doch schon 12 Jahre alte Rechner mit der richtigen Software (y-cruncher oder ymp) 10 Mio. Stellen in unter 1 s berechnen können:
https://www.lamprechts.de/csv/2-Sqrt(14).zip