Bestimmen Sie die Länge der Seite y sowie die (exakten) Winkel β und δ im

Question

   

Es seien: 
α = \( \frac{π}{6} \) , γ = \( \frac{5π}{6} \)  , c = 2 , b = \( \sqrt{3} \)  , x= 2

gegeben. Bestimmen Sie die Länge der Seite y sowie die (exakten) Winkel β und δ im
Bogenmaß.

vielen Dank

Comments

Hatten wir diese Frage nicht gerade schon ?

(und die Zeichnung ist immer noch gleich irreführend ...)

---

echt? konnte sie nicht finden...

---

Vom Duplikat:

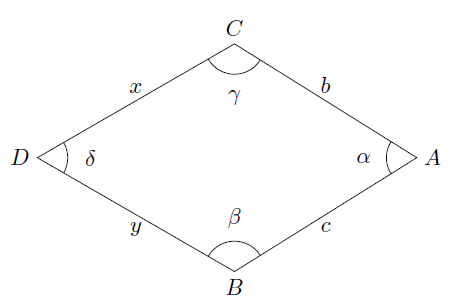
Titel: Bestimmen Sie die Länge der Seite y sowie die (exakten) Winkel β und δ im Bogenmaß.

Stichworte: sinus,cosinus

Es seien
$$ \alpha=\frac{\pi}{6}, \quad \gamma=\frac{5 \pi}{6}, \quad c=2, \quad b=\sqrt{3}, \quad x=2 $$
gegeben. Bestimmen Sie die Länge der Seite \( y \) sowie die (exakten) Winkel \( \beta \) und \( \delta \) im Bogenmaß.

---

https://www.mathelounge.de/729604/komme-restlichen-werte-heran-unbrauchbare-werte-bekommen

Answer 1

Das Viereck ist ein Parallelogramm wegen α + γ = π und c = x.

Comments

WIe berechnet man die seiten b und y??????????????

---

Man überlegt sich, welche Eigenschaften Parallelogramme haben. Unter Anderem sind da zu nennen:

        Gegenüberliegende Seiten sind gleich lang

        Gegenüberliegende Winkel sind gleich groß

---

Ehhhmmm.. Hast du die aufgabe überhaupt gelesen??

die seiten,  b und y sind nicht gegeben!!!!!!!!!!!!!!

---

Die Länge der Seite b ist gegeben. Schau dazu noch mal genau in deine Frage, ob du da so etwas wie \(b=\dots\) erkennen kannst.

---

ja habs erkannt.