Hallo Clara,
mal angenommen, da sind drei Messwertpaare \((x_1,y_1)\), \((x_2,y_2)\) und \((x_3;y_3)\). Das Modell für den Zusammenhang von \(x\) zu \(y\) ist $$y(x) = ax^2 + y_0$$\(y_0\) ist bereits gegeben. Nun soll ein Wert für \(a\) bestimmt werden, dass die Abweichungen \(r_i\) zum Modell möglichst klein sind. Das wäre$$r_1 = ax_1^2 + y_0 - y_1 \\ r_2 = ax_2^2 + y_0 - y_2\\ r_3 = ax_3^2 + y_0 - y_3$$und das Ziel ist es die Summe \(S\) der Quadrate der Abweichungen zu minimieren$$S = r_1^2 + r_2^2 + r_3^2 \to \min$$Man kann nun in die Gleichung für \(S\) die obigen Ausdrücke einsetze und dann nach \(a\) ableiten, um den 'optimalen' Wert für \(a\) zu berechnen.
Ein wenig anschaulicher wird es, sich das ganze vektoriell vorzustellen. Die obigen drei Gleichungen kann man auch schreiben$$\begin{pmatrix} r_1 \\ r_2 \\ r_3\end{pmatrix} = \begin{pmatrix} x_1^2 \\ x_2^2 \\ x_3^2\end{pmatrix} \cdot a - \begin{pmatrix} y_1 -y_0\\ y_2 -y_0 \\ y_3 -y_0 \end{pmatrix}$$ bzw. $$\vec r = \vec{\varphi(x)} \cdot a - \vec y$$das \(\vec{\varphi(x)}\) ist der Vektor aus allen \(x_i^2\) und das \(S\) ist das Quadrat der Länge von \(\vec r\). Und das Ziel ist es, dass dieser Vektor \(\vec r\) bzw. seine Länge möglichst kurz wird.
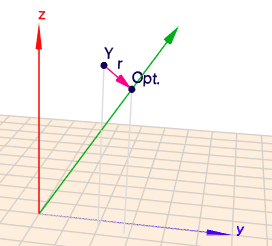
Oben habe ich das nochmal graphisch dargestellt. Der grüne Vektor ist \(\vec{\varphi(x)}\) und der steht gleichzeitig für die Geradengleichung $$\vec {x(a)} = \vec{\varphi(x)} \cdot a $$Gesucht ist der Punkt \(\vec{x(a_{opt})}\) für den der Vektor \(\vec r = \vec{x(a_{opt})} - \vec y\) möglichst kurz ist. Dies ist genau dann erreicht, wenn \(\vec r\) und \(\vec{\varphi(x)}\) senkrecht auf einander stehen - daraus folgt:$$\begin{aligned} \vec{\varphi(x)}^T \cdot \vec r &= 0 \\ \vec{\varphi(x)}^T (\vec{\varphi(x)} \cdot a - \vec y) &= 0 \\ \vec{\varphi(x)}^T \cdot \vec{\varphi(x)} \cdot a&= \vec{\varphi(x)}^T \cdot \vec y\end{aligned}$$und dies ist die Normalengleichung, die man allgemein als \(A^TA \alpha = A^T y\) schreibt. In unserem Fall ist die Matrix \(A\) nur eindimensional und somit ein Vektor, was die Sache stark vereinfacht. Das ist natürlich das gleiche Ergebnis, was man erhält, wenn man oben das \(S\) nach \(a\) ableitet und zu 0 setzt.
Machen wir mal ein Zahlenbeispiel, \(y_0\) sei \(y_0=2\) und die drei Messwerte sind: $$\begin{array}{} x_i& y_i \\ \hline1& 2.5\\ 2& 4\\ 2.5& 7\end{array}$$Die 'Matrix' \(A\) ist hier der Vektor mit den X-Quadraten und von den \(y_i\) müssen wir noch das \(y_0=2\) subtrahieren:$$A= \begin{pmatrix}1\\ 4\\ 6.25\end{pmatrix}, \quad y = \begin{pmatrix}0.5\\ 2\\ 5\end{pmatrix}$$Mit den Zahlenwerten gibt das $$\begin{aligned} \begin{pmatrix}1& 4& 6.25\end{pmatrix} \cdot \begin{pmatrix}1\\ 4\\ 6.25\end{pmatrix} \cdot a &= \begin{pmatrix}1& 4& 6.25\end{pmatrix} \cdot \begin{pmatrix}0.5\\ 2\\ 5\end{pmatrix}\\ 56,0625 \cdot a &= 39,75 \\ \implies a &\approx 0,7090\end{aligned}$$und im Graphen sieht es so aus:
~plot~ {1|2.5};{2|4};{2.5|7};0.709x^2+2;[[-5|9|-1|9]] ~plot~
Die Daten im ersten Bild stammen aus diesem Beispiel. Wenn Du auf das Bild klickst, kannst Du die Szene mit der Maus drehen und bekommst einen besseren räumlichen Eindruck.
Gruß Werner