Berechne C und D eines Rechtecks ABCD

Question

A(0/-2/8) B(-2/2/4) bilden zwei Ecken eines Rechtecks ABCD, von dem C auf der x-Achse liegt.

- Berechne C und D.

Answer 1

Nach Kommentar verbessert! Richtungsvektor BC war verkehrt aufgestellt.

BA = [2, -4, 4]
BC = [x + 2, -2, -4]

[2, -4, 4]·[x + 2, -2, -4] = 0 → x = 2

C = [2, 0, 0]

D = C + BA = [4, -4, 4]

https://www.matheretter.de/rechner/schragbild?draw=viereck(0%7C-2%7C8%20-2%7C2%7C4%202%7C0%7C0%204%7C-4%7C4)&scale=10&pa=45&xy=1

Comments

BC = [x, 2, -8]

so steht \(AC \perp AB\) und nicht \(BC \perp AB\) ! Das Ergebnis ist $$C = \begin{pmatrix}2\\ 0\\ 0\end{pmatrix}$$ im Schrägbild sieht man das nicht, in Geoknecht3D schon:

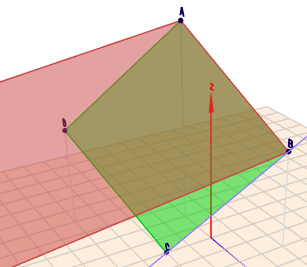
das grüne Viereck ist ein Rechteck (sogar ein Quadrat) - das rote ist nur ein Parallelogramm.

---

Vielen Dank für den Hinweis. Ich hatte zwar Richtungsvektor BC korrekt geschrieben aber AC aufgestellt. Ich habe es jetzt verbessert.