L-periodische Fortsetzung einer Funktion (Fourier-Reihe)

Question

Aufgabe:

$$\text{ In dieser Aufgabe geht es um die L-periodische Fortsetzung der Funktion  }$$

$$f(x)=1-2\Theta(x-L/2) für x\in\left[0,L\right)$$

$$\text{ a) Skizzieren Sie diese Funktion für ein paar Perioden. }$$

$$\text{ b) Zeigen Sie, dass der Mittelwert } f_{0}\text{ dieser Funktion 0 ist. }$$

$$\text{ c) Bestimmen Sie die Fourier-Koeffizienten }c_{n}\text{ dieser Funktion. }$$

$$\text{ d) Geben Sie die Fourier-Koeffizienten  }a_{n}\text{ und }b_{n} $$

$$\text{ an und schreiben Sie die Reihe als Summe von Sinus und Cosinus Funktionen. }$$

$$\text{ e) Skizzieren Sie die ersten 2 Terme der Reihe }$$

Problem:

Mit diesem Thema habe ich leider allgemein meine Schwierigkeiten weshalb ich um Hilfe bei dieser Aufgabe sehr dankbar wäre.

Comments

wie ist Θ(x) denn definiert?

lul

---

$$\Theta(x)\text{ ist Definiert als die Theta-Funktion }\int_{x}^{-∞}dy δ(y)=\{\text{ 0 für } x<0 ;\text{ 1 für } x>0\}= \Theta(x)$$

---

Vom Duplikat:

Titel: Sägezahn- und Heaviside-Funktion

Stichworte: stetigkeit,mittelwert,reihen

Θ ist in dieser Aufgabe die Heaviside-Funktion.

Diese bereitet mir allerdings so einige Schwierigkeiten.

Also meine Überlegungen sind Folgende:

a)

Eine Funktion mit der Periode L heißt dies: f(x) = f(x + L)

x geht ja von einschließlich 0 bis nicht einschließlich L.

Für x würde ich jetzt einfach zum Plotten eine Wertetabelle aufstellen.

Aber wie lasse ich das nicht einschließlich L mit einfließen?

b)

Der Mittelwert wird wie folgt berechnet:

f₀ = \( \frac{1}{L} \) * \( \int\limits_{0}^{L} \) dx f(x)

Laut Wikipedia ist die Stammfunktion der Heaviside-Funktion = max { 0,x } + C, damit kann ich allerdings leider so gar nichts anfangen.

c)

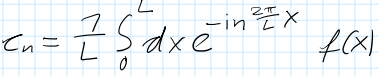
So kann ich C_n bestimmen, allerdings stehe ich hier wieder vor dem Problem der mir nicht ganz verständlichen Stammfunktion der Heaviside-Funktion.

d)

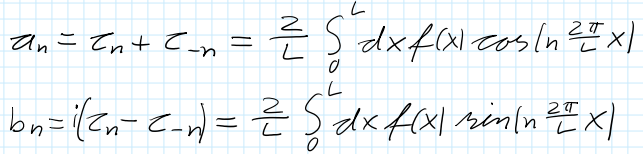
Selbes Problem, das Werkzeug besitze ich, allerdings scheitert es erneut an meinem Verständnis der Stammfunktion der Heaviside-Funktion.

e)

Basiert auf d).

Bonuspunkt:

Da mir die restlichen Ergebnisse fehlen konnte ich noch keine Überlegungen dazu anstellen.

Für Tipps oder Hilfestellungen wäre ich wirklich sehr dankbar!

---

Hallo

 da ich das schon in einem anderen thread beantwortet habe, guck erstmal. ob dir das reicht.

https://www.mathelounge.de/739126/l-periodische-fortsetzung-einer-funktion-fourier-reihe#a739211

Gruß lul

Answer 1

Hallo

 soweit ich sehe kannst du f(x) auch schreiben: f(x)=1 die 0<=x<L/2 und f(x)=-1 für L/2<=x<L und dann periodisch , d.h es ist eine ungerade Funktion du brauchst nur die Koeffizienten von  sin zu bestimmen. dass der Mittelwert 0 ist die orientierte Fläche d.Hh das Integral von 0 bis L von f(x)=0

jetzt nur diese einfache Funktion , in die Formeln für die Fourrierreihe einsetzen, Wo kann man da noch Schwierigkeiten haben?

 Gruß lul

Comments

Danke das hat mir sehr geholfen :)