Hallo,
a) Wenn P auf der Verbindungsstrecke der Mittelpunkte der Seiten AB und CD des Trapezes liegt, haben die Dreiecke ADP und BCP den gleichen Flächeninhalt.
Die Mitten von \(AB\) und \(CD\) seien \(E\) und \(F\).
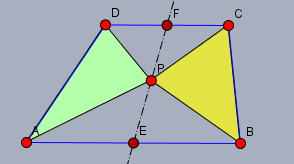
Wenn \(P\) auf der Strecke \(EF\) liegt, dann ist die Fläche \(F_{\triangle DAP}\) des grünen Dreiecks $$F_{\triangle DAP} = F_{AEFD} - F_{\triangle AEP} - F_{\triangle FDP}$$nun ist aber wegen \(|AE| = |EB|\) und \(|CF| = |FD|\)$$\begin{aligned} F_{AEFD} &= \frac 12(|AE| + |FD|) h = \frac 12(|EB| + |CF|)h = F_{EBCF} \\ F_{\triangle AEP} &= F_{\triangle EBP} \\ F_{\triangle FDP} &= F_{\triangle CFP}\end{aligned}$$Und daraus folgt$$\begin{aligned} F_{\triangle DAP} &= F_{AEFD} - F_{\triangle AEP} - F_{\triangle FDP} \\&= F_{EBFC} - F_{\triangle EBP} - F_{\triangle CFP} \\&= F_{\triangle BCP} \end{aligned}$$ und \(F_{\triangle BCP}\) ist das gelbe Dreieck rechts.
b) Wenn die Flächeninhalte der Dreiecke DAP und BCP gleich groß sind, dann liegt P auf der Verbindungsstrecke der Mittelpunkte von AB und CD.
Wenn \(F_{\triangle DAP} = F_{\triangle BCP}\), dann gilt genau wie oben unabhängig von der Lage von \(P\) die Gleichheit der Flächen der zwei Dreiecke unten \(F_{\triangle AEP} = F_{\triangle EBP}\) und zwei Dreiecke oben \(F_{\triangle FDP} = F_{\triangle CFP}\) und die Gleichheit der Trapeze \(F_{AEFD} = F_{EBCF}\), die unabhängig von \(P\) sind.

Aus der Gleichheit der Dreiecksflächen folgt auch die Gleichheit der Summe $$\begin{aligned} F_{\triangle DAP} + F_{\triangle AEP} + F_{\triangle FDP} &= F_{\triangle BCP} + F_{\triangle EBP} + F_{\triangle CFP} \\&= \frac 12 F_{ABCD} \\&= F_{AEFD} \end{aligned}$$wenn aber das Fünfeck \(AEPFD\), welches sich aus den drei Dreiecken zusammen setzt, genauso groß ist, sie das Trapez \(AEFD\), so muss die Fläche des Dreiecks \(\triangle EFP\) gleich 0 sein$$F_{\triangle EFP} = 0 \implies P \in EF$$somit liegt \(P\) auf der Verbindungsstrecke \(EF\).