Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.

Question

Aufgabe:leider verstehe ich diese Aufgaben nicht

Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.

a.) Die Tangente an den Graphen im Punkt P(0/0) hat die Steigung 0. Die Steigung der Tangente im Punkt Q(-3/0) beträgt 6.

b.) Der Punkt P(1/4) ist ein Extrempunkt, der Punkt Q(0/2) ein Wendepunkt des Graphen.

Answer 1

a) f(x) = ax^3+bx^2+cx+d

f(0) =0

f '(0) = 0

f(-3) =0

f '(-3) = 6

b)

f(1) =4

f '(1) = 0

f(0) = 2

f ''(0) = 0

Stelle je 4 Gleichungen auf.

Answer 2

a)

f(0)=0

f'(0)=0

f(-3)=0

f'(-3)=6

b)

f(1)=4

f'(1)=0

f(0)=2

f''(0)=0

Answer 3

Nutze: http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

a.) Die Tangente an den Graphen im Punkt P(0/0) hat die Steigung 0. Die Steigung der Tangente im Punkt Q(-3/0) beträgt 6.

b.) Der Punkt P(1/4) ist ein Extrempunkt, der Punkt Q(0/2) ein Wendepunkt des Graphen.

Answer 4

Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.

(0)        f(x) = ax³ + bx² + cx + d

Die Tangente an den Graphen im Punkt P(0/0)

Die Funktion verläuft durch den Punkt (0/0). Also ist

        f(0) = 0

und somit

(1)        a·0³ + b·0² + c·0 + d = 0.

hat die Steigung 0

Also ist auch

        f'(0) = 0.

Wegen

        f'(x) = 3ax² + 2bx + c

ist also

(2)        3a·0² + 2b·0 + c = 0

Die Steigung der Tangente im Punkt Q(-3/0) beträgt 6.

Das liefert dir wie oben zwei Bedingungen

        f(-3) = 0

und

        f'(-3) = 6.

Stelle daraus die Gleichungen (3) und (4) auf.

Löse das Gleichungssystem, das aus den Gleichungen (1), (2), (3) und (4) besteht. Setze die Lösung in (0) ein um die Funktionsgleichung zu bekommen.

b.) Der Punkt P(1/4) ist ein Extrempunkt, der Punkt Q(0/2) ein Wendepunkt des Graphen.

Prinzipiell genau so wie a.)

Comments

Ich bin dir echt dankbar nur sitz ich hier seit 20 Minuten und verstehe nicht richtig wie ich die Gleichung angehen soll, weil man Mathe Lehrer leider zu inkompetent ist um zu erklären :0

---

wie ich die Gleichung angehen soll

Welche Gleichung meinst du? Und was meinst du genau mit "angehen"? Hast du die Gleichungen (3) und (4) schon aufgestellt?

Answer 5

"Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.
a.) Die Tangente an den Graphen im Punkt P(0|0) hat die Steigung 0. Die Steigung der Tangente im Punkt Q(-3|0) beträgt 6."

Lösung über die Nullstellenform der kubischen Parabel:

doppelte Nullstelle Extremwert bei P(0|0) und einfache Nullstelle bei Q(-3|0):

f(x)=a*[x^2*(x+3)]

Tangente im Punkt Q(-3|0) beträgt 6:

f´(x)=a*[2x*(x+3)+x^2*1]

f´(-3)=a*[2(-3)*(-3+3)+(-3)^2]=a*9

9a=6 → a=\( \frac{2}{3}\)

f(x)=\( \frac{2}{3}\)*x^2*(x+3)

Comments

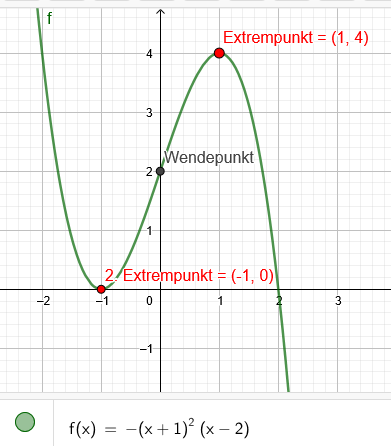
b.) "Der Punkt P(1|4) ist ein Extrempunkt, der Punkt Q(0|2) ein Wendepunkt des Graphen."

Da der Punkt Q(0|2) der Wendepunkt und P(1|4) ein Extrempunkt des Graphen ist liegt der 2. Extremwert bei R(-1|0)

Lösung wieder über die Nullstellenform:

\(f(x)=a*(x+1)^2*(x-N)\)

\(P(1|4)\)

\(f(x)=a*(1+1)^2*(1-N)=4a*(1-N)\)

\(4a*(1-N)=4→a=\frac{1}{1-N}\)

\(f(x)=\frac{1}{1-N}*[(x+1)^2*(x-N)]\)

Extremwerteigenschaft bei \(P(1|4)\):

\(f´(x)=\frac{1}{1-N}*[(2x+2)*(x-N)+(x+1)^2]\)

\(f´(1)=\frac{1}{1-N}*[(2+2)*(1-N)+(1+1)^2]\)

\(\frac{1}{1-N}*[4*(1-N)+4]=0→N=2\)

\(a=\frac{1}{1-2}=-1\)

\(f(x)=-(x+1)^2*(x-2)\)