Gleichung der ganzrationalen Funktion 3.Grades.

Question

Aufgabe:leider verstehe ich diese Aufgaben nicht

Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.

a.) Die Tangente an den Graphen im Punkt P(0/0) hat die Steigung 0. Die Steigung der Tangente im Punkt Q(-3/0) beträgt 6.

b.) Der Punkt P(1/4) ist ein Extrempunkt, der Punkt Q(0/2) ein Wendepunkt des Graphen.

Problem/Ansatz:

a) f(x) = ax3+bx2+cx+d

f(0) =0

f '(0) = 0

f(-3) =0

f '(-3) = 6

b)

f(1) =4

f '(1) = 0

f(0) = 2

f ''(0) = 0

Mein Problem die Gleichung kann mir da bitte jemand Aufgabe a vorrechnen, damit ich weiß was ich zu tun habe, da ich die Erklärung meines Mathe Lehrers überhaupt nicht verstanden habe

Comments

Hast du meine Lösungen verstanden? Sonst frag nach.

:-)

Answer 1

f(x)=ax^3+bx^2+cx+d

f'(x)=3ax^2+2bx+c

a)

f(0)=0 → d=0

f'(0)=0 → c=0

f(-3)=0 → 0= -27a+9b → b=3a

f'(-3)=6 → 6= 27a-6b → 6=27a-18a → 6=9a

a=2/3

b=2

f(x)=2/3*x^3+2x^2

b)

f(1)=4 → 4=a+b+c+d

f'(1)=0 → 0= 3a+2b+c

f(0)=2 → d=2

f"(0)=0 → b=0

Also

4=a+c+2

0=3a+c

Zweite minus erste Gleichung

-2=2a → a=-1 → c=3

f(x)=-x^3+3x+2

Answer 2

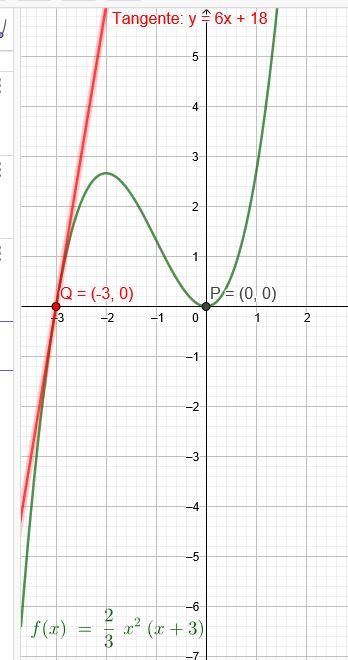
Bestimmen Sie die Gleichung der ganzrationalen Funktion 3.Grades.

a.)Die Tangente an den Graphen im Punkt \(P(0|0)\) hat die Steigung 0. Die Steigung der Tangente im Punkt \(Q(-3|0)\) beträgt 6.

doppelte Nullstelle in \(P(0|0)\) wegen Steigung 0

einfache Nullstelle in \(Q(-3|0)\)

Nullstellform der kubischen Parabel:

\(f(x)=a*x^2*(x-(-3))=a*[x^2*(x+3)]\)

Tangentensteigung \(m=6\)

\(f´(x)=a*[2x*(x+3)+x^2*1]\)

\(f´(-3)=a*[2*(-3)*(-3+3)+(-3)^2]=9a=6\)   \(a=\frac{2}{3}\)

\(f(x)=\frac{2}{3}*x^2*(x+3)\)

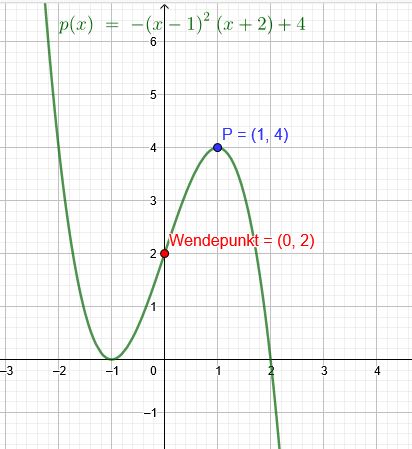
b.) Der Punkt \(P(1|4)\) ist ein Extrempunkt, der Punkt \(Q(0|2)\) ein Wendepunkt des Graphen.

Ich verschiebe den Graph um 4 Einheiten nach unten:
\(P(1|4)\)→\(P´(1|0)\) doppelte Nullstelle wegen Extrempunkt
\(f(x)=a*(x-1)^2*(x-N)\)
\(Q(0|2)\) → \(Q´(0|-2)\)
\(f(0)=a*(0-1)^2*(0-N)=-a*N=-2\)  \(a=\frac{2}{N}\)
\(f(x)=\frac{2}{N}*[(x-1)^2*(x-N)]=\frac{2}{N}*[(x^2-2x+1)*(x-N)]\)
Wendepunkt \(f´´(x)=0\):

\(f´(x)=\frac{2}{N}*[(2x-2)*(x-N)+(x^2-2x+1)]\)

\(f´´(x)=\frac{2}{N}*[2*(x-N)+(2x-2)+(2x-2)]=-\frac{2}{N}*[2*x-2N+2x-2+2x-2]=-\frac{2}{N}*[6*x-2N-4]\)

\(f´´(0)=\frac{2}{N}*[-2N-4]\)

\(\frac{2}{N}*[-2N-4]=0\)→\(N=-2\)     \(a=-1\)

\(f(x)= -(x-1)^2*(x+2) \)

um 4 Einheiten nach oben:

\(p(x)= -(x-1)^2*(x+2)+4 \)