Zu 1a und 1b und 1f)
Hier das Koordinatensystem mit den eingetragenen Werten und dem Graphen der in Aufgabe e bestimmten Funktion (eventuell solltest du die Skalierung noch etwas verfeinern):
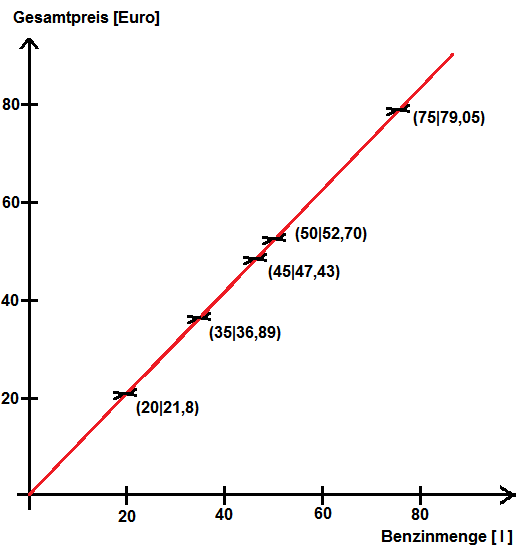
(Bei dem ersten Preis des ersten Wertepaares habe ich ein kleines Problem - er scheint mir etwas zu hoch zu sein. Na, das werden wir später sehen ...)
Zu 1c)
Es besteht ein proportionale Zusammenhang zwischen den Werten genau dann, wenn es eine konstante Zahl c gibt, sodass für alle Wertepaare ( x | y ) gilt:
y / x = c
Also fangen wir oben an:
79,05 / 75 = 1,054
52,70 / 50 = 1,054
47,43 / 45 = 1,054
36,89 / 35 = 1,054
21,80 / 20 = 1,090
Also: Für alle Wertepaare bis auf das Paar ( 20 | 21,80 ) ergibt sich die Konstante Zahl c = 1,054. Beim ersten Wertepaar scheint also wie vermutet ein Fehler vorzuliegen. Geht man davon aus, dass tatsächlich 20 Liter getankt wurden, dann hätte der Preis
x / 20 = 1,054 <=> x = 20 * 1,054 = 21,08
sein müssen, damit sich auch bei diesem Wertepaar die Konstante c = 1,054 ergibt. Es sieht also so aus, als hätte der Tabellenersteller die Null hinter dem Komma vergessen ...
Nun, nehmen wir also an, dass tatsächlich das Wertepaar ( 20 | 21,08 ) gemeint gewwesen sei.
Wie man sieht, ist also der Quotient x / y für alle Wertepaare ( x | y ) gleich 1,054. Genau das aber ist ein Kriterium dafür, dass eine proportionaler Zusammenhang zwischen den Wertepaaren besteht.
1d)
Die Konstante c heißt "Proportionalitätsfaktor" (gelegentlich auch "Proportionalitätskonstante"). Da bei seiner Berechnung der Gesamtpreis in Euro durch das getankte Volumen in Litern dividiert wurde, trägt er die Einheit [ Euro / l ]. Seine Bedeutung ist also der Preis pro Liter. Dieser beträgt im vorliegenden Beispiel sagenhaft niedrige 1,054 Euro / l .
1e)
Der Funktionsterm einer proportionalen Funktion hat die Form
f ( x ) = c * x
wobei c der Proportionalitätsfaktor ist. Die Funktion f ( x ) liefert den Gesamtpreis in Euro für x Liter, also nenne ich sie Gesamtpreis ( x ). Es gilt:
Gesamtpreis ( x ) = 1,054 * x
Überprüfung z.B. des dritten Wertepaares ( 45 | 47,43 ):
47,43 = 1,054 * 45
Das ist eine wahre Aussage, also erfüllt das Wertepaar die Funktionsgleichung.
1f) (siehe oben)
1g)
Gesamtpreis ( 65 ) = 1,054 [Euro / l] * 65 [l] = 68,51 [Euro]
Prüft man das Wertepaar ( 65 | 68,51) mit dem oben gezeigten Graphen nach, dann stellt man fest, dass dieser Punkt ebenfalls auf dem Graphen liegt.
1h)
Hier ist der Gesamtpreis gegeben. Es soll also bestimmt werden, wieviel Liter Benzin man dafür bekommt. Es gilt also:
Gesamtpreis ( x ) = 57,97 = 1,054 * x
<=> x = 57,97 / 1,054 = 55 [l]
Prüft man das Wertepaar ( 55 | 57,97) mit dem oben gezeigten Graphen nach, dann stellt man fest, dass dieser Punkt ebenfalls auf dem Graphen liegt.