Modulo Gruppentafel erstellen

Question

Aufgabe: Erstelellen einer Gruppentafel mit \((\mathbb{Z}/7\mathbb{Z},+)\)

Problem/Ansatz:

Wie erstellt man diese

Answer 1

Deine Menge hat nur sieben Elemente: \(\mathbb{Z}/7\mathbb{Z}=\left \{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4},\overline{5},\overline{6}\right \}\)

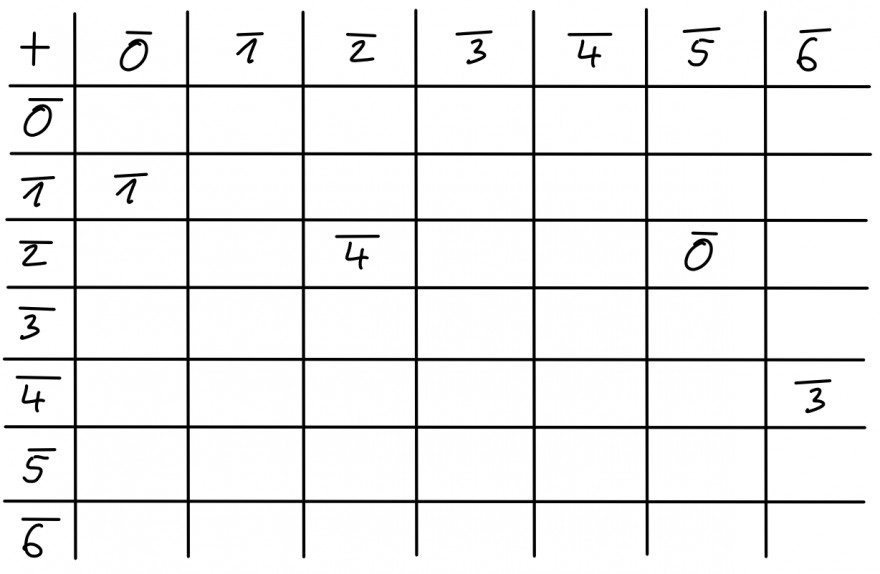
Auf \(\mathbb{Z}/m\mathbb{Z}\) ist für alle \(m\in \mathbb{N}_{>0}\) eine Addition durch \(\overline{x}+\overline{y}:=\overline{x+y}\) gegeben, wobei \(x,y\in \mathbb{Z}\).

Für die ersten Einträge ist also:

\(\overline{1}+\overline{0}=\overline{1+0}=\overline{1}\)

\(\overline{2}+\overline{2}=\overline{2+2}=\overline{4}\)

\(\overline{2}+\overline{5}=\overline{2+5}=\overline{7}=\overline{0}\)

\(\overline{4}+\overline{6}=\overline{4+6}=\overline{10}=\overline{3}\)

Außerdem bildet diese Addition auf Restklassen eine abelsche Gruppe, weshalb du dich nur auf den oberen oder unteren Dreiecksbereich konzentrieren musst und du den Rest symmetrisch übertragen kannst.

Comments

Danke für Ihre Antwort

Nach ihrer Antwort sollte ich sagen ,ob dir Restklasse eine Gruppe ist oder kommutativ Nach Der Erstellung des Tafels

---

Ok, dann musst du es halt komplett ausrechnen. Dann wirst du anhand der Gruppenaxiome sehen können, dass man mit dieser Addition eine Gruppe bildet, und sogar eine abelsche, was sich durch die Symmetriegestalt der Gruppentafel zeigt.

---

Es war eine Frage ,ob ich sagen sollte

---

Es war eine Frage ,ob ich sagen sollte

Dann formuliere bitte dein Kommentar als Frage und nicht als unvollständigen Satz. Und ob es eine Gruppe ist, wirst du an der Tafel ablesen können. Sonst wäre es sinnlos, eine Gruppentafel zu machen, wenn man bereits wüsste dass \((\mathbb{Z}/7\mathbb{Z},+)\) eine abelsche Gruppe bildet. Das sollst du aber erstmal mit der Tafel überprüfen.