Hallo Jasmin,
a) Bitte beschreiben Sie, was der Begriff , Lineare Unabhängigkeit" dreier Vektoren im \(\mathbb R^3\) mit der Lösbarkeit eines linearen Gleichungssystems zu tun hat!
Ich habe die drei Vektoren \(\vec a\), \(\vec b\) und \(vec c\) mal im Geoknecht3D eingegeben:
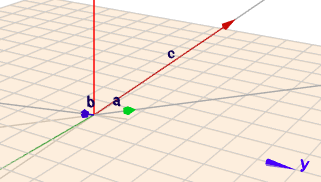
(klick auf das Bild und rotiere die Szene mit Maus. Dann bekommst Du einen räumlichen Eindruck)
Mit Hilfe folgender Linearkombination, das ist eine Summe von Vielfachen der drei Vektoren, kann man in diesem konkreten Fall jeden Punkt im Raum erreichen. $$\vec p = \begin{pmatrix}1\\ 2\\ 1\end{pmatrix} u + \begin{pmatrix}2\\ 1\\ 1\end{pmatrix} v + \begin{pmatrix}-5\\ 2\\ 2\end{pmatrix} w$$Das geschieht durch geeignete Wahl der drei Parameter \(u\), \(v\) und \(w\). Nehmen wir als Beispiel mal $$\begin{pmatrix}1\\ 2\\ 1\end{pmatrix} u + \begin{pmatrix}2\\ 1\\ 1\end{pmatrix} v + \begin{pmatrix}-5\\ 2\\ 2\end{pmatrix} w = \begin{pmatrix}5,5\\ -1\\ 0\end{pmatrix}$$Jetzt steht dort ein lineares Gleichungssystem, was man auch so schreiben könnte:$$\begin{pmatrix}1& 2& -5\\ 2& 1& 2\\ 1& 1& 2\end{pmatrix} \cdot \begin{pmatrix}u\\ v\\ w\end{pmatrix} = \begin{pmatrix}5,5\\ -1\\ 0\end{pmatrix}$$Im 3D-Modell sieht das so:
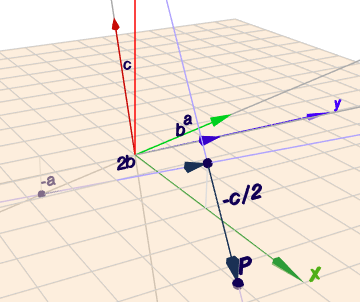
dort siehst Du den Weg, über Vielfache der drei Vektoren vom Ursprung hin zum Punkt \(P\). Es ist $$\vec p = -1 \cdot \vec a + 2 \cdot \vec b - \frac 12 \vec c$$
Wenn nun aber die drei Vektoren in einer Ebene liegen würden .. so wie hier
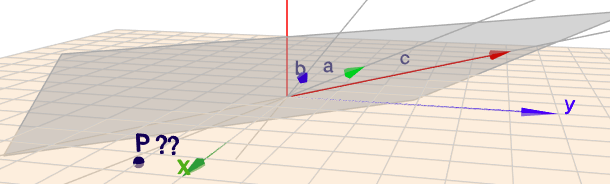
.. dann gibt es keine Möglichkeit, egal welche Werte man für die drei Parameter wählt, den Punkt \(P\) zu erreichen.
Hier kann man jeden der drei Vektoren über eine Linearkombination der beiden anderen darstellen. Es gibt also eine Lösung für $$\vec c = u \cdot \vec a + v \cdot \vec b$$D.h. die drei Vektoren sind nicht mehr linear unabhängig und somit ist ein beliebiger Punkt nicht mehr zwingend zu erreichen, also ist das LGS nicht eindeutig lösbar.
bei b ist das richtig berechnet?
Na ja - Du hast nicht zu Ende gerechnet. Grundsätzlich solltest Du versuchen, die Matrix in eine Stufenform zu bringen. D.h. im unteren linken Dreieck der Matrix sollten Nullen stehen. Ausgehed von$$\begin{pmatrix}1& 2& -5\\ 2& 1& 2\\ 1& 1& 2\end{pmatrix}$$sollen in der ersten Spalte ab der zweiten Zeile Nullen stehen. Ziehe dazu das doppelte der ersten Zeile von der zweiten und die erste Zeile von der dritten ab (\(II \to II - 2 \cdot I\) und \(III \to III - I\)) $$\begin{pmatrix}1& 2& -5\\ 0& -3& 12\\ 0& -1& 7\end{pmatrix}$$Normiere die zweite Zeile, indem Du diese durch \(-3\) dividierst:$$\begin{pmatrix}1& 2& -5\\ 0& 1& -4\\ 0& -1& 7\end{pmatrix}$$so bleibt auf der Hauptdiagonalen ein \(1\) stehen. Addiere nun die zweite Zeile zur dritten, so dass das Element unter der \(1\) zu \(0\) wird$$\begin{pmatrix}1& 2& -5\\ 0& 1& -4\\ 0& 0& 3\end{pmatrix}$$Nun hast Du eine Stufenform erreicht, mit Nicht-Null-Elementen auf der Hauptdiagonalen. Das ist der Beleg, dass die drei Spaltenvektoren linear unabhängig sind.