Größtmöglicher Widerstandswert

Question

Aus einem Baumstamm mit kreisförmigen Querschnitt soll ein Balken mit rechteckigem Querschnitt so herausgeschnitten werden, dass ein Widerstandsmoment W = (1/6)bh² den größtmöglichen Wert annimmt (d.h. der Balken soll so stabil wie möglich sein). Berechnen Sie b und h in Abhängigkeit von d so, dass W maximal wird.

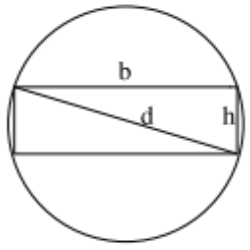
b: Breite des Balkens, h: Höhe des Balkens, d: Durchmesser des Baumstamms

Answer 1

b^2 + h^2 = d^2
h^2 = d^2 - b^2

W(b, h) = 1/6 bh^2
W(b) = 1/6 b(d^2 - b^2)
W(b) = 1/6 (bd^2 - b^3)

W'(b) = 1/6(d^2 - 3b^2)
W''(b)= -b

W' = 1/6(d^2 - 3b^2) = 0
d^2 - 3b^2 = 0
b = ±d/√3
b = d/√3 (negative breite sinnfrei ist)

W''(d/√3) = -d/√3 < 0 ⇒ b = d/√3 ist maximum

h^2 = d^2 - b^2
h = √(d^2 - b^2)
h = √(d^2 - (d/√3)^2)
h = d √(2/3)