Bedinge Wahrscheinlichkeiten ( Baumdiagramm)

Question

Bei einem Skatspiel erhält jeder der drei Spieler 10 Karten; die restlichen beiden Karten werden in den Skat gelegt.

Felix hat genau 2 Buben und 8 weitere Karten auf der Hand und hofft, dass genau ein weiterer Bube im Skat liegt. Welche Wahrscheinlichkeit besteht hierfür?

Ich muss es mithilfe eines Baumdiagrams lösen.
Ich dachte mir, dass ich nur den Skat betrachten soll. Da hat man entweder einen Buben oder eben keinen; wenn man einen schon hat, dann hat man schon den Buben, den Felix braucht, deswegen würde ich nichts weiteres dranzeichnen.
Wenn die 1. Karte aber kein Buben ist, kann ja die 2. immer noch ein Buben (oder auch keinen) sein.

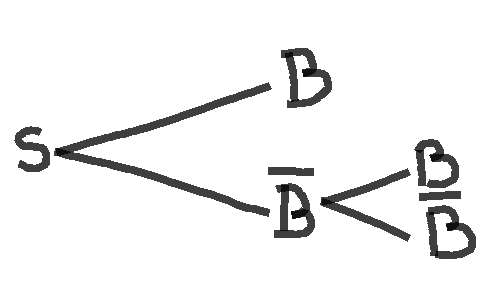
Von diesen Gedanken ausgehend hätte ich den Baum wie im Abb. gezeichnet. Allerdings weiß ich nicht genau, welche Wahrscheinlichkeiten ich dran schreiben soll (theoretisch hat man ja bei dem 1. 1/2 für die beide Fälle, da man ja entweder Buben hat oder nicht? aber ich weiß nicht, ob das Sinn ergibt?) oder ob mein Ansatz überhaupt stimmt

:)

Answer 1

bei dem 1. 1/2 für die beide Fälle, da man ja entweder Buben hat oder nicht?

Mit diesem Argument ist die Wahrscheinlichkeit, im Lotto den Jackpot zu knacken 1/2 weil man ja entweder den Jackpot knackt oder nicht.

Es gibt 22 Karten, die Felix nicht hat.

Unter diesen 22 Karten befinden sich 2 Buben.

Die Wahrscheinlichkeit, dass die erste Karte im Skat ein Bube ist, ist 2/22.

Falls die erste Karte im Skat ein Bube ist, dann ist die Wahrscheinlichkeit, dass die zweite Karte im Skat ebenfalls ein Bube ist, 1/21. Andernfalls ist sie 2/21.

Comments

Ja das mit Lotto stimmt schon, ich meinte eher, weil es im Skat nur 2 Karten gibt; 1 davon müsste wohl entweder Buben oder kein Buben sein (laut meiner Gedanken)
:)