Baumdiagramm x1 und x2 Berechnung

Question

Text erkannt:

Bercchine dic

Aufgabe:

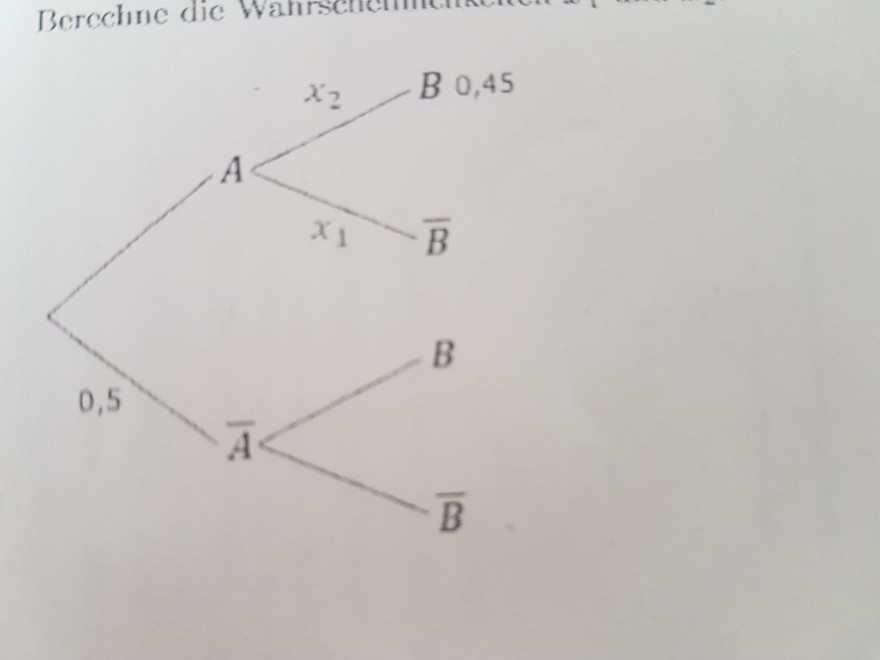
Ein Baumdiagramm mit den Wahrscheinlichkeiten :

P (¯A) =0,5     P(A∩B)= 0,45

Die Wahrscheinlichkeiten x1 und x2 sollen bestimmt werden

      

    
Problem/Ansatz:

B ist bereits mit 0,45 angegeben ( gehört doch zu x2 ,oder?, weil es auf einem Pfad ist.)

Dann müsste   ¯B demanch 0,55 sein? (damit es auf 1 kommt) oder liege ich da falsch?

Wie würde man ansonsten noch x1 und x2 berechnen? Ich liege da gerade echt auf dem Schlauch und wäre für jede Hilfestellung sehr dankbar.

mfg

Answer 1

Hallo,

mit den 0,55 liegst du richtig, in der 1. Stufe ist der unbeschriftete Pfad dann auch 0,5.

Entlang der Pfade wird multipliziert. Wenn du also bereits Anfangs- und Endwahrscheinlichkeiten hast, musst du dividieren.

Gruß, Silvia

Comments

Vielen Dank für die Rückmeldung

Answer 2

Sei x₁=x. Dann gilt 0,5x=0,45 und x=0,9.

Dann ist x₂=1-x=1-0,9=0,1.

Comments

Vielen Dank. Eine Frage habe ich zu diesem Rechenweg, wie sind Sie für x2 =1-x gekommen?

---

x₁+x₂ =1 also x₂=1-x₁.  

Answer 3

P(A)=1-0,5=0,5

0,45=P(A)*x₂=0,5*x₂

x₂ = 0,9

x₁=1- x₂=1-0,9=0,1