Vektoren Lösen mit Matrix

Question

Aufgabe:

Gegeben sind die Vektoren:

\( \overrightarrow{\mathrm{a}}=\left(\begin{array}{l}2 \\ 3 \\ 2\end{array}\right), \overrightarrow{\mathrm{b}}=\left(\begin{array}{l}3 \\ 4 \\ 1\end{array}\right), \overrightarrow{\mathrm{c}}=\left(\begin{array}{l}2 \\ 4 \\ 6\end{array}\right) \) und \( \overrightarrow{\mathrm{d}}=\left(\begin{array}{c}2 \\ 3 \\ -3\end{array}\right) \)

a) Zeigen Sie, dass ein mit \( \vec{a}  , \vec{b} \) und \( \overrightarrow{\text { c }} \) als Koeffizientenvektoren und \( \overrightarrow{\mathrm{d}} \) als Ergebnisvektor aufgestelltes Gleichungssystem keine Lösung hat!

b) Welchen Wert muss die erste Komponente \( d_{1} \) des Vektors \(\vec{d}\) haben, damit das dadurch entstehende neue Gleichungssystem unendlich viele Lösungen hat \( \left(\mathrm{d}_{2}\right. \) und \( \mathrm{d}_{3} \) sollen nicht verändert werden!)?

c) Berechnen Sie eine dieser Lösungen!

Problem/Ansatz:

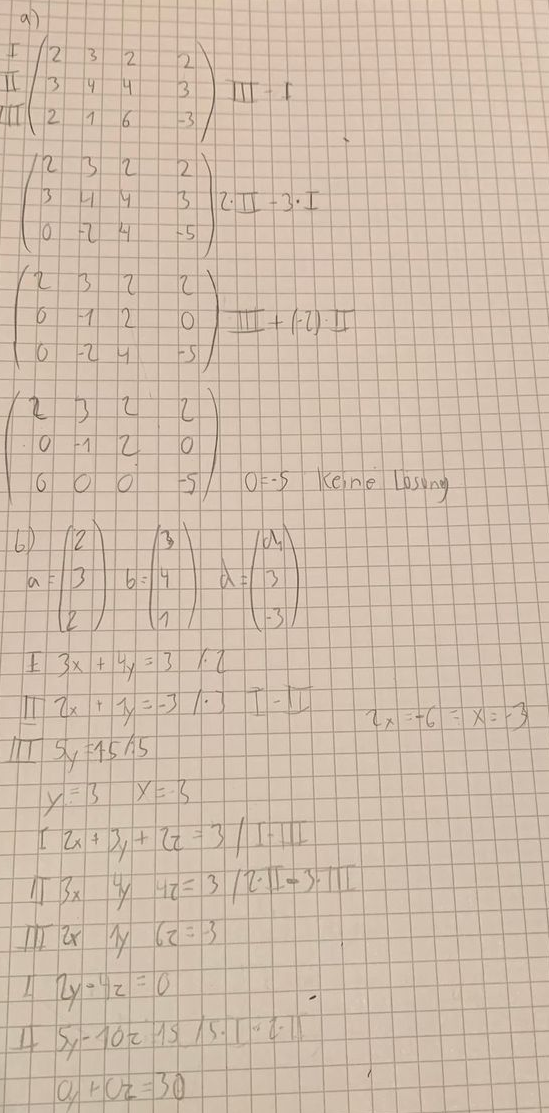
Ich glaube a ist richtig aber bei b rechne ich glaube ich ins leere. kann mir jemand erklären was ich falsch gemacht habe?

Answer 1

Hallo,

a) sieht richtig aus. Bei b) vergisst du, den Vektor \(\vec{c}\) mit einzubeziehen. Du musst also stattdessen dieses LGS betrachten:

\(x\cdot \left(\begin{array}{l}2 \\ 3 \\ 2\end{array}\right)+y\cdot \left(\begin{array}{l}3 \\ 4 \\ 1\end{array}\right)+z\cdot \left(\begin{array}{l}2 \\ 4 \\ 6\end{array}\right)=\left(\begin{array}{c} d_1 \\ 3 \\ -3\end{array}\right)\)

und dann lösen.