Bedingte Wahrscheinlichkeiten - gut und schlecht abschneiden.

Question

Aufgabe:

Sandra schneidet in 60% der Fälle gut (+) ab, ansonsten schlecht (-). Sie hat bemerkt, dass sie bei Prüfungen gut abschneidet, wenn sie am Morgen Tee (T) trinkt. Die Ereignisse + und T scheinen stochastisch unabhängig zu sein.

a) Skizziere eine Vierfeldertafel. Gib dabei Wahrscheinlichkeiten an, die zu dieser Situation passen.

b) Berechne vier bedingte Wahrscheinlichkeiten und erläutere deren Bedeutung.

c) Untersuche die Aussage: Wenn die Ereignisse + und T unabhängig sind, dann sind auch - und T' unabhängig.

Problem/Ansatz:

Bitte um Hilfe bei der Lösung der Aufgabe.

Comments

Stell´einmal ein Foto der Aufgabe ein.
Irgendwie scheinen Angaben zu fehlen.

---

Hallo,

ich versuche vergeblich aus der Galerie das Foto der Aufgabe hier einzufügen. Ich habe allerdings gerade nochmal kontrolliert, ob alles aus dem Arbeitsblatt abgeschrieben ist und alles stimmt.

In der letzten Zeile habe ich mit T' das Gegenereignis von T gemeint.

VG

---

Bei der Frage kann ich dir leider nicht helfen
mfg Georg

---

Danke trotzdem.

VG

Answer 1

a) Skizziere eine Vierfeldertafel. Gib dabei Wahrscheinlichkeiten an, die zu dieser Situation passen.

Wo liegt genau das Problem? Du darfst dir hier doch sogar passende Wahrscheinlichkeiten ausdenken.

Ich skizziere es mal wie es aussehen könnte.

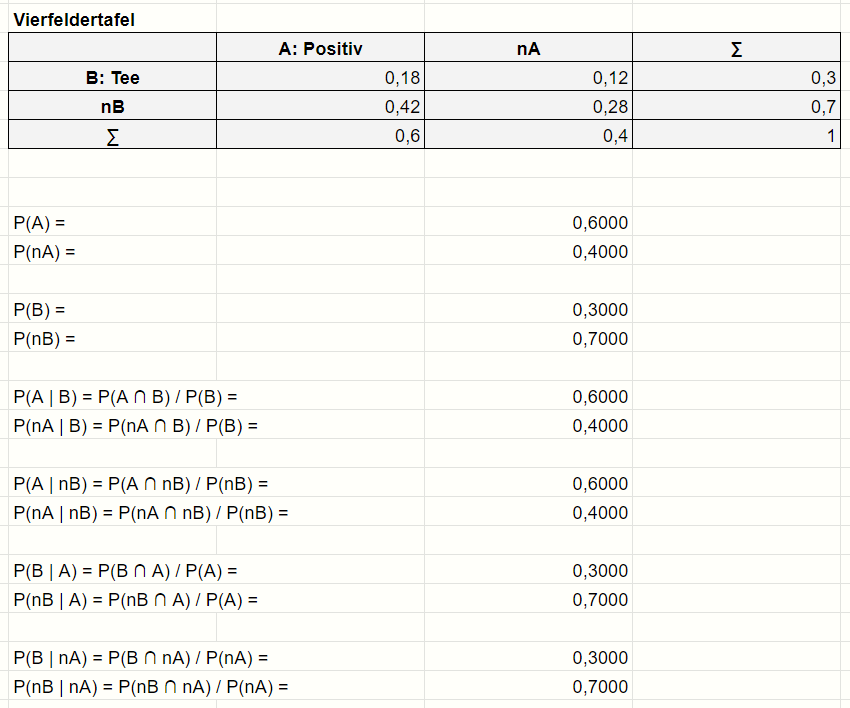
b) Berechne vier bedingte Wahrscheinlichkeiten und erläutere deren Bedeutung.

Ich habe die wichtigsten bedingten Wahrscheinlichkeiten gleich mit berechnet.

Erläutern schaffst du selber oder brauchst du da auch hilfe?

c) Untersuche die Aussage: Wenn die Ereignisse + und T unabhängig sind, dann sind auch - und T' unabhängig.

Kannst du die Formel für die Unabhängigkeit aufstellen und es prüfen? Du solltest feststellen das auch - und T' unabhängig sind

Comments

Vielen Dank,

ich sollte den Rest schon selbst hinkriegen.

VG