f(x)=a*x^3+b*x^2+c*x+d
P (1/4) liegt auf f(x)
1.)
f(1)=a*1^3+b*1^2+c*1+d
a*1^3+b*1^2+c*1+d=4
Q(0|2) liegt auf f(x)
2.)
f(0)=a*0^3+b*0^2+c*0+d
d=2
P (1/4) ist ein Extremwert
f´(x)=3 a*x^2+2b*x+c
3.)
f´(1)=3 a*1^2+2b*1+c
3 a*1^2+2b*1+c=0
Nun weiter mit der 2.Ableitung zum Wendepunkt.
mfG
Moliets
Ein weiterer Weg:
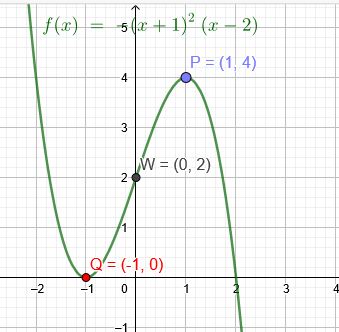
\(P(1|4)\) und \(W(0|2)\) → \(Q(-1|0)\) doppelte Nullstelle
\(f(x)=a(x+1)^2(x-N)\)
\(W(0|2)\):
\(f(0)=a(0+1)^2(0-N)=2 \) \(a=-\frac{2}{N}\)
\(f(x)=-\frac{2}{N}(x+1)^2(x-N)\)
\(P(1|4)\):
\(f(1)=-\frac{2}{N}(1+1)^2(1-N)=-\frac{8}{N}(1-N)\)
\(-\frac{8}{N}(1-N)=4\) \(N=2\) \(a=-1\)
\(f(x)=-(x+1)^2(x-2)\)
.