Fläche und Umfänge von Kreisfiguren

Question

In den Skizzen sind zwei kongruente Quadrate der Seitenlänge \( 4 \mathrm{~cm} \) dargestellt. E, F, G. H sind die Mittelpunkte der Quadratseiten.

B. G. E sind die Mittelpunkte der entsprechenden Kreisbögen, \( \mathbf{M} \) ist der Mittelpunkt des Kreises.

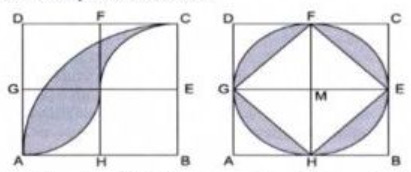
a) Zeige, dass die beiden grau getonten Figuren den gleichen Flicheninhalt besitzen.

b) Um wie viel \( \mathrm{cm} \) ist der Umfang der zweiten Figur lainger als der der ersten?

Answer 1

A1 = 1/4·pi·4^2 - 1/4·pi·2^2 - 2^2 - (2^2 - 1/4·pi·2^2) = 4·pi - 8

A2 = pi·2^2 - 1/2·4^2 = 4·pi - 8

U1 = 1/4·2·pi·4 + 1/2·2·pi·2 = 4·pi

U2 = 2·pi·2 + 4·√(2^2 + 2^2) = 4·pi + 8·√2

U2 - U1 = 8·√2 = 11.31 cm

Answer 2

Hallo

 

Bild linke Seite:

Fläche AK des Viertelkreises mit Mittelpunkt B:
AK = 1/4 * 4^2*pi = 1/4 * 16 * pi = 4*pi
Flächeninhalt Ak des Viertelkreises mit Mittelpunkt E
Ak = 1/4 * 2^2*pi = 1/4 * 4*pi = pi
Das ist auch der Flächeninhalt des Viertelkreises um G

A1 = 4^2 - AK = 16 - 4*pi
A2 = Ak = pi
A3 = 2^2 = 4
A4 = 2^2 - Ak = 4 - pi

Der Flächeninhalt A der getönten Fläche berechnet sich:

A = 4^4 - A1 - A2 - A3 - A4
A = 16 - (16 - 4*pi) - pi - 4 - (4 - pi)
A = 16 - 16 + 4*pi - pi - 4 - 4 + pi
A = 4*pi - 8

Bild rechte Seite:

Der Flächeninhalt A der getönten Fläche ist der Flächeninhalt des Kreises AK
minus Flächeninhalt Aq des Quadrates.
A = AK - Aq

AK = 2^2*pi = 4*pi
Aq = 8
A = AK - Aq =  4*pi - 8

Offensichtlich haben die grau getönten Flächen den gleichen Flächeninhalt.

Gruß
gorgar