Wie lang ist die Leiter? Satz des Pythagoras

Question

Aufgabe:

Eine Leiter ist genauso lang wie eine Mauer hoch ist. Lehnt man diese Leiter 20 cm unter dem oberen Mauerrand an, so steht sie unten 1.20 m von der Mauer entfernt. Wie lang ist die Leiter?

Answer 1

Hi,

ich habe Dir hier mal eine Zeichnung. Solltest Du bei solchen Aufgaben selbst machen :).

Nun ganz richtig den Pythagoras verwenden:

x^2+120^2 = (x+20)^2

x^2+120^2 = x^2+40x+20^2  |-x^2-20^2

40x = 120^2-20^2 = 14400-400 = 14000  |:40

x = 350

 

Die Leiter ist also y = (350 + 20) cm = 3,7 m lang.

Grüße

Answer 2

Hallo alligator,

 

nennen wir die Länge der Leiter und die Höhe der Mauer x.

Dann haben wir in etwa folgendes rechtwinklige Dreieck:

 

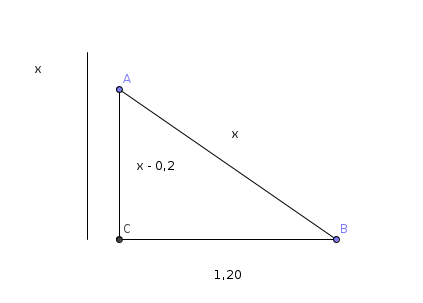
Darauf wenden wir den Satz des Pythagoras an:

1,20² + (x - 0,2)² = x²

1,20² = x² - (x - 0,2)²

1,20² = x² - (x² - 0,4x + 0,04)

1,20² = x² - x² + 0,4x - 0,04

1,44 = 0,4x - 0,04

1,48 = 0,4x

3,7 = x

 

Die Leiter ist also 3,70 m lang.

 

Probe:

3,50² + 1,20² = 12,25 + 1,44 = 13,69

3,70² = 13,69

 

Besten Gruß