Schnellskizzen, Manipulation des Graphen

Question

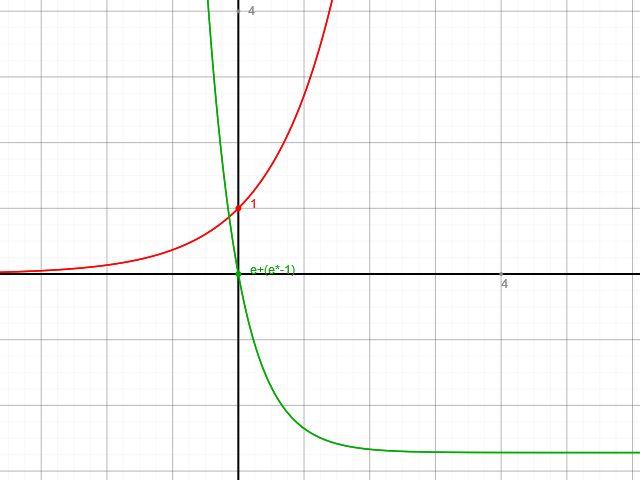
meine Aufgabe ist es anhand der Funktion f(x)=e^{1-2x}-e darzustellen, wie die Grundfunktion des Graphen manipuliert wurde.

Die Grundfunktion ist meiner Ansicht nach e^x.

Manipulationen:

- Verschiebung um -e nach unten (entlang der y-Achse)

-Spiegelung durch neagtives e im Exponenten

Sind die zwei Merkmale so richtig?

Der manipulierte Graph ist ja gestreckt, aber um welchen Faktor?

 

Danke für die Hilfe und viele Grüße !

 

David

 

Comments

Hallo David,

  der grüne Graph zeigt aber nicht die Funktion f(x)=e^1-2x- e.

  Welche Funktion meinst du ? Bitte einmal eindeutig angeben.

  mfg Georg

---

Hallo Georg,

die Beschriftung des Graphens ist meiner Meinung nach fehlerhaft. Ich meine genau die Funktion

f(x)= e^1-2x-e, wie oben beschrieben.

Der Graph von  f(x)=e^1-2x- e verläuft auch laut geogebra genau so... Wieso die Beschriftung hier so komisch ist, kann ich mir nicht erklären.

 

mfG

David

Answer 1

hi

"Sind die zwei Merkmale so richtig?"

ja. :-)

"Der manipulierte Graph ist ja gestreckt, aber um welchen Faktor?"

e^1-2x= e^-x • e^-x • e = e^-x • k(x)

als faktor in der gespiegelten variante könnte man hier k(x) = e^-x • e ansehen. die (gespiegelte) grundfunktion multipliziert mal sich selbst, mal e ≈ 2,718.

Answer 2

Hallo David,

  ich bin folgendermaßen vorgegangen :

  Grundfunktion : e^x   l  * e^x ergibt
  e^2x  l dies entspricht im Graphen einer Stauchung mit dem Faktor 2
  dann den Kehrwert bilden :
  1 / e^2x  l dies entspricht im Graphen einer Spiegelung  an der y-Achse
  die Konstante 1 abziehen
  1 / e^2x  - 1 l dies  entspricht im Graphen einer Verschiebung nach unten
  dann das Ganze mal dem konstanten Faktor e nehmen
  ( 1 / e^2x  - 1 ) * e  l dies entspricht einer Streckung in Y-Richtung

  anders geschrieben lautet der Term auch
  e^{1-2x} - e
  also dein Ausgangsterm.

  mfg Georg