Bestimmung einer Siebenecks

Question

Aufgabe:

Noch eine neue Aufgabe der Woche. Ganze Aufgabe steht auf dem Bild

Problem/Ansatz:

Bitte die ganze Aufgabe, ausführlich wenn möglich. Bitteee!

Text erkannt:

Aufgabe der Woche
Aufgabe 1

In einem regelmäßigen Siebeneck mit der Seitenlänge \( 2 \mathrm{cm} \) sind die Diagonalen a und b gegeben. Bestimme \( \frac{1}{a}+\frac{1}{b} \)
Aufgabe 2
Einem Halbkreis ist ein Trapez umbeschrieber in dem die Längen der zueinander parallelen Seiten gegeben sind. Bestimme den Inhalt der gefärbten Fläche.

Comments

2)   Wie groß ist r?

mfG

Moliets

---

Wie groß ist r

Es ist wohl Teil der Aufgabe, das zu berechnen.

Answer 1

Hallo,

Ein Winkel \(\alpha\) im regelmäßigen Siebeneck hat den Wert $$\alpha = 180° - \frac {360°}7 = \frac {900°}7 \approx 128,6°$$

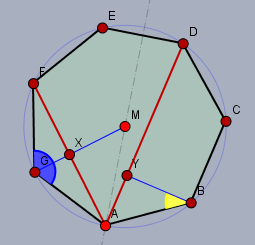
Das ist der blaue Winkel in der Zeichnung oben. Die Strecke \(a\) berechnet sich aus$$a = |AF| = 2|AX| = 2 s \cdot \sin\left( \frac \alpha 2 \right) \approx 3,6 \text{cm}$$ Das Viereck \(ABCD\) ist ein symmetrisches Trapez. Die Grundseite \(b\) berechnet sich aus$$b = |AD| = 2\cdot \left( |AB| \cdot \sin(\alpha - 90°) \right) + |BC| = s (2 \sin(\alpha - 90°) + 1) \approx 4,5 \text{cm}$$und $$\frac 1a + \frac 1b = \frac 12 \text{cm}^{-1}$$

Bei der Aufgabe 2 kannst Du ausnutzen, dass die beiden markierten Dreiecke hier ...

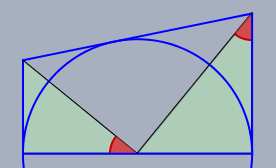
... ähnlich sind, da der rot markierte Winkel der selbe ist. Ist der Radius des Kreises \(r\) so gilt demnach $$\frac{2 \sqrt 3}{r} = \frac {r}{3 \sqrt 3}$$falls Du noch Fragen hast, so melde Dich bitte.

Comments

Der Lösungsweg zu 1) tut physisch weh (Näherungswerte führen zum genauen Ergebnis).

Mit den beiden Hilfslinien erhalten wir gleichschenklige und einander ähnliche Dreiecke mit a:b = 2:(b-2). Das lässt sich mit etwas Geschick und ohne zweifelhafte Näherungswerte bis nach 1/a + 1/b = 1/2 bringen.

---

Sehr gut abakus! Danach habe ich gesucht, aber ich hatte es nicht gefunden ;-)

---

Danke.

Bei 2) hast du übrigens recht mit

Bei der Aufgabe 2 kannst Du ausnutzen, dass die beiden markierten Dreiecke hier ähnlich sind

aber hoffentlich merkt die Fragestellerin, dass auch diese Aussage eine (noch)  unbewiesene Hypothese ist. Eine Verbindungslinie von Kreismittelpunkt zum oberen Berührungspunkt eröffnet da ganz neue Perspektiven.

---

dass auch diese Aussage eine (noch)  unbewiesene Hypothese ist

trifft auch auf die (wahrscheinlich richtige) Annahme zu, dass die blauen Flächenteile Kreissektoren sind

---

Wie soll man dann bei der 2 die flächeninhalt ausrechnen bitte komplett

---

Wie soll man dann bei der 2 die flächeninhalt ausrechnen bitte komplett

Aus diesem Zusammenhang $$\frac{2 \sqrt 3}{r} = \frac{r}{3 \sqrt 3}$$folgt \(r^2 = 18\). Und da der Winkel des weißen Sektors \(=90°\) ist (warum?) haben die beiden blauen Sektoren zusammen die Fläche eines Viertelkreises.

Also ist die gefärbte Fläche \(A\) $$A =  \frac 14 A_{\text{Kreis}} = \frac 14 \pi r^2 = \frac 92 \pi$$

Answer 2

Das ist wohl eine Art Wettbewerbsaufgabe. Daher gebe ich nur mal zwei Tipps ab und lasse meine Gedankengänge weg.

1. 1/a + 1/b = 0.5

2. A = 4.5·pi