Weg-Zeit Aufgabe: Wann fährt der zweite PKW los?

Question

Aufgabe:

Ein Pkw fährt mit einer konstanten
Geschwindigkeit von 50 km/h. Ein zweiter Pkw fährt mit
80 km/h los, nachdem der erste bereits 20 km gefahren
ist. Wann fährt der zweite PKW los? Zeichne das
zugehörige s-t-Diagramm und bestimme damit, nach wie vielen Minuten der 2. PKW ihn einholt.

Problem/Ansatz:

Ich weiß nicht, wie ich das ausrechnen kann bzw. falls es stimmt was ich vermute habe ich immer noch Probleme dabei die Gleichung aufzulösen.

Also kann es sein, dass man die Daten vom 1. PKW in v= s/t einfügen soll?

Answer 1

$$t_0/20km= 60min/50km$$

$$t_0=24min$$

$$80/60(t-24)=20+50/60*(t-24)$$

$$t=24+60*20/30min= 64min$$

Answer 2

Hallo,

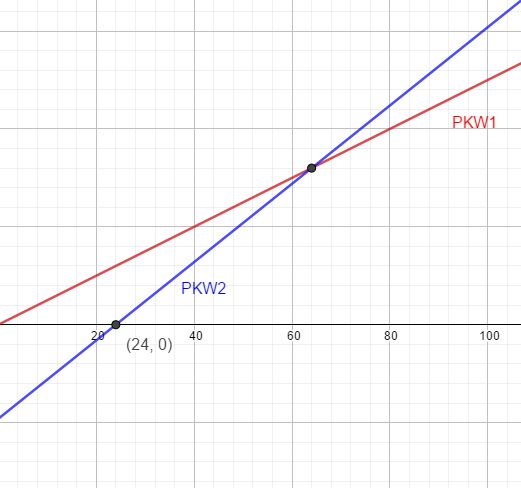
du berechnest zunächst den Zeitpunkt, an dem PKW 2 losfährt bzw. nach wieviel Minuten PKW1 20 km weit gekommen ist.

$$\text{50 km }\hat=\text{ 60 min}\\\text{1 km }\hat=\frac{6}{5}\text{ min}\\\text{20 km }\hat=\text{ 24 min}$$

Die Gleichung für PKW1 lautet y = 50x

und für PKW2 y = (x - 24)·80

Um den Schnittpunkt zu bestimmen, setzt du die Gleichungen gleich und löst nach x auf:

50x = (x - 24)·80

x = 64