Aufgabe:
Text erkannt:
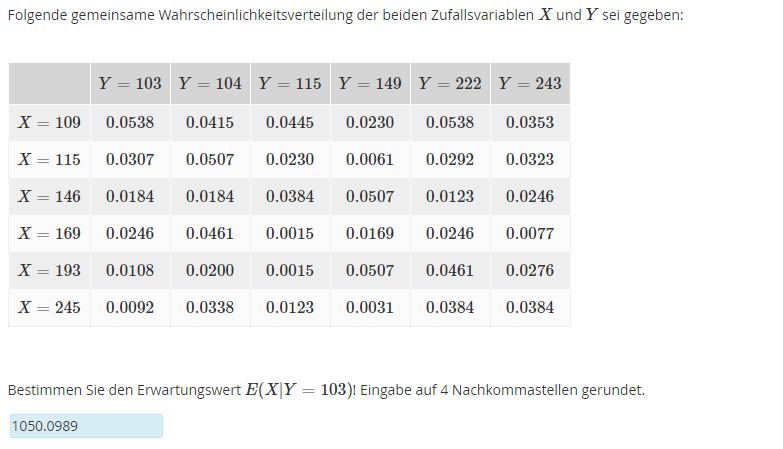
Folgende gemeinsame Wahrscheinlichkeitsverteilung der beiden Zufallsvariablen \( X \) und \( Y \) sei gegeben:
\begin{tabular}{lcccccc}
& \( Y=103 \) & \( Y=104 \) & \( Y=115 \) & \( Y=149 \) & \( Y=222 \) & \( Y=243 \) \\
\hline\( X=109 \) & 0.0538 & 0.0415 & 0.0445 & 0.0230 & 0.0538 & 0.0353 \\
\( X=115 \) & 0.0307 & 0.0507 & 0.0230 & 0.0061 & 0.0292 & 0.0323 \\
\( X=146 \) & 0.0184 & 0.0184 & 0.0384 & 0.0507 & 0.0123 & 0.0246 \\
\( X=169 \) & 0.0246 & 0.0461 & 0.0015 & 0.0169 & 0.0246 & 0.0077 \\
\( X=193 \) & 0.0108 & 0.0200 & 0.0015 & 0.0507 & 0.0461 & 0.0276 \\
\( X=245 \) & 0.0092 & 0.0338 & 0.0123 & 0.0031 & 0.0384 & 0.0384
\end{tabular}
Bestimmen Sie den Erwartungswert \( E(X \mid Y=103) \) । Eingabe auf 4 Nachkommastellen gerundet.
1050.0989
Problem/Ansatz:
Bei Aufgaben wo E(Y|X=n) da rechne ich einfach die Wahrscheinlichkeiten von z.B. Y=103 = (0.0538+...)*103 und dass bei allen Zahlen und am Schluss addieren.
Diese Zahl dann dividiert mit der Wahrscheinlichkeiten von X=n d.h. 0.0xxx+....
Die Obere Zahl habe ich mit der unteren beschriebenen Zahl Dividiert. Und das Ergebnis war richtig.
Jetzt bei dieser Aufgabe ist E(X|Y=n) gesucht und ich komme auf E(X)=154.8896 und E(Y=103)=0.1462. Diese zwei dividiert ergeben 1050.098983 = 1050.0990. FALSCH
Wird diese Aufgabe anders gelöst oder bin ein Depp und vertippe mich immer beim Rechnen?