Punkt bestimmen Graph

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x) = 1/4x^2-2, x e r

A) Bestimmen ie den Punkt, in dem der Graph von f die Steigung 3 hat.

Problem/Ansatz:

Ich verstehe nicht, wie ich vorgehen muss

Answer 1

f '(x)=1/2·x es soll 3=1/2·x sein. das ist für x=6 der Fall. f(6)=7.

Im Punkt (6|7) hat der Graph von f die Steigung 3 .

Comments

Gibt es ein Video, welches Sie mir zu diesem Thema empfehlen könnten?

Answer 2

Ein Zugang ohne Ableitung:

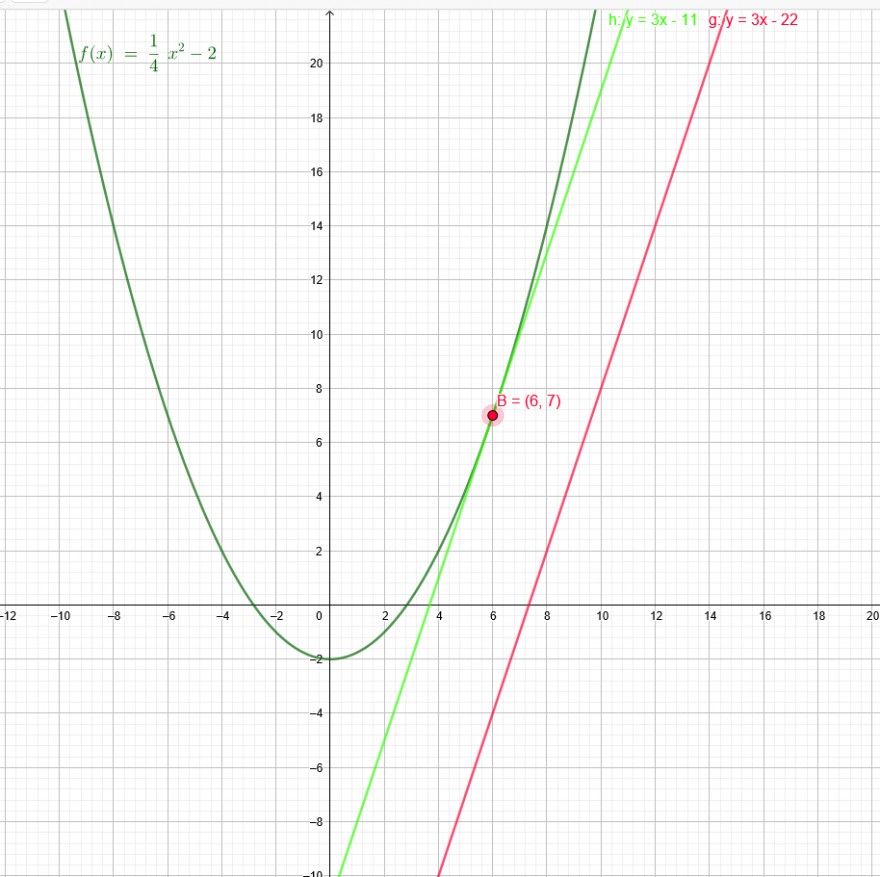
f(x)=1/4x^2-2

Steigung in B→ m=3

Ich wähle eine Gerade mit der Steigung m=3, welche die Parabel nicht schneidet:

g(x)=3x-22

\( \frac{1}{4} \) x^2-2=3x-22

1/4x^2=3x-20|*4

x^2-12x=-80|+q.E.(-\( \frac{12}{2} \) ) ^2= (-6)^2 = 36

x^2-12x+36=-80+36

(x-6)^2 =-44= 44*i^2

x_1=6+sqrt(44*i^2)

x_2=6-sqrt(44*i^2)

Der Berührpunkt liegt somit bei B(6|7)

mfG

Moliets