Kanonenkugel - Bewegung

Question

Weiß jemand, wie man wir verfährt?

Aus einem Kanonenrohr werden Kanonenkugeln mit fester Anfangsgeschwindigkeit \( v_{0} \) geschossen, wobei der Winkel zur Horizontalen beliebig gewählt werden kann. Das Gravitationsfeld wird als homogen angenommen und Reibung wird vernachlässigt.
(a) Welche Maximalhöhe kann die Kanonenkugel erreichen?
(b) Was ist die maximale horizontale Reichweite \( d_{0} \) der Kanonenkugel? Welchen Winkel muss man dazu einstellen?
(c) Welchen Winkel muss man einstellen, damit eine vorgegebene horizontale Reichweite \( d_{1}<d_{0} \) erreicht wird?

Answer 1

Hier meine Meinung

alpha : Abschußwinkel
v0 : Anfangsgeschwindigkeit
s Flugstrecke = v0 * t
sv ; Flugstrecke in vertikaler Richtung ( nach oben )
( siehe Skizze )
Anstelle von tan(a) ist sin(a) richtig
Strecke durch Erdanzieheng : s = 1/2 * g * t^2

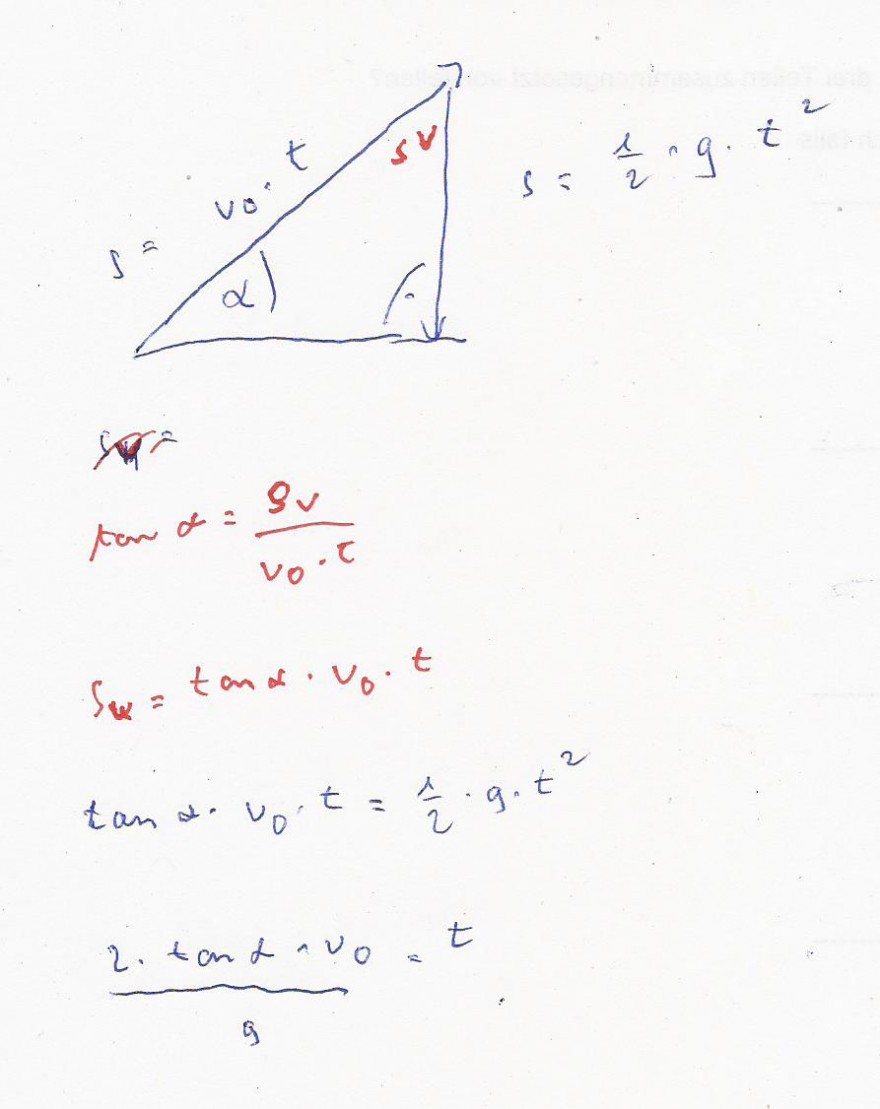
anstelle von tan(a) ist sin(a) richtig
sin ( a ) = sv / ( v0 * t )
sv = sin(a) * v0 * t

sin(a) * v0 * t = 1/2 * g * t^2
t = 2 * sin(a) * v0 / g

Die Flugzeit ist von alpha und Anfangsgeschwindigkeit
abhängig.

(a) Welche Maximalhöhe kann die Kanonenkugel erreichen?
Maximalhöhe bei Schuß nach oben.
sin(90) = 1
v0 * t = 1/2 * g * t^2
t = 2 * v0 / g
h = v0 * t
h = v0 * 2 * v0 / g
Die maximalhöhe ist nur von der Abschußgeschwindigkeit
abhängig.

Soviel zunächst.

mfg Georg

Comments

Ich danke dir!

---

Deine SKizze hat mir geholfen, dass anschaulich zu verstehen, danke

---

Gern geschehen.
Falls Fragen offen sind ( b , c )
dann frage nach.

Answer 2

a)

Energieerhaltungssatz

1/2·m·v^2 = m·g·h --> h = v^2/(2·g)

Und zwar bei einem Abschusswinkel von 90°. Aber Achtung. Nach dem Schuss sollte man sich unverzüglich verdrücken.

Comments

Vielen Dank!