Innermathematisches mit e funktionen

Question

Hallo, ich habe folgende Aufgabe, welche ich leider absolut nicht verstehe;

Aufgabe:

1) Unter der Randfunktion f(x)= e^-x soll ein Rechteck wie in der Abbildung skizziert so eingebaut werden, dass es maximalen Flächeninhalt hat. Begründen Sie zunächst anschaulich, dass es ein Rechteck mit maximalem Flächeninhalt geben muss. (Siehe Abbildung)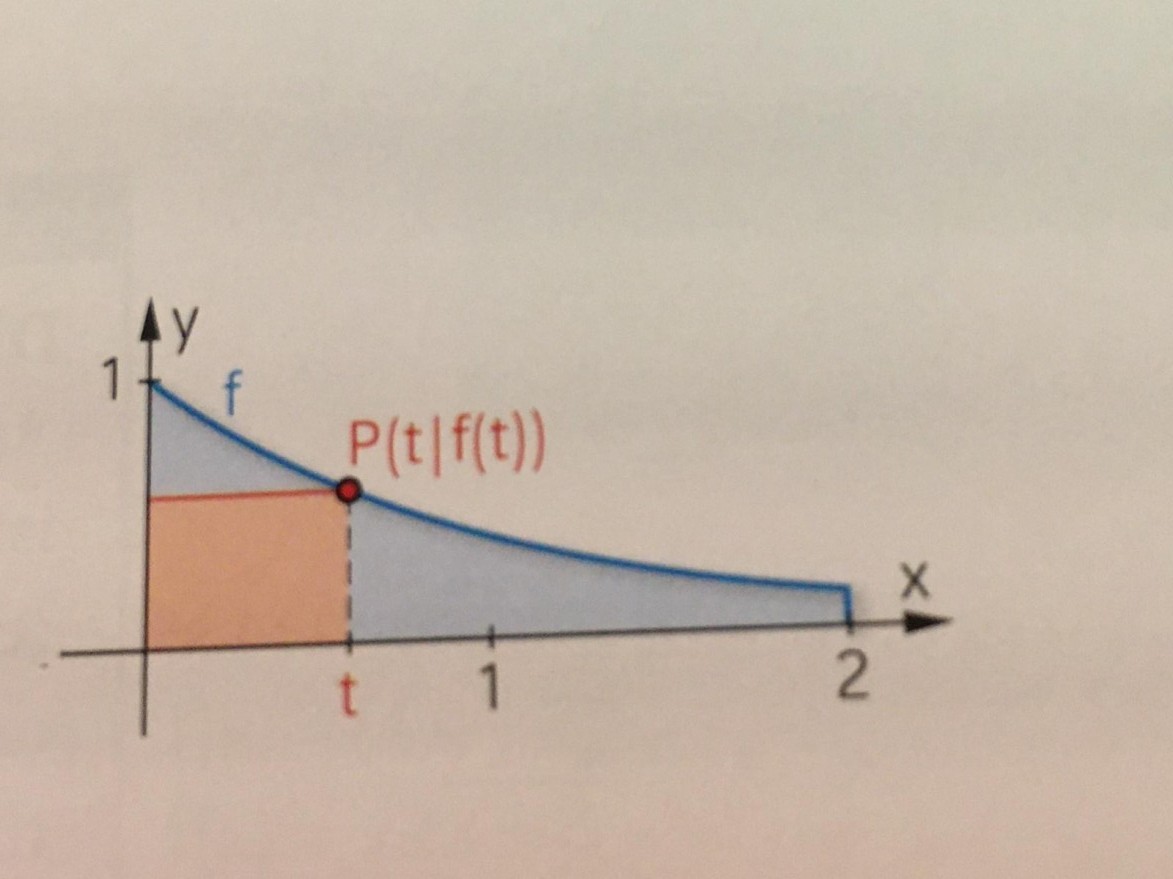

Problem/Ansatz:

Ich habe leider keinen Ansatz, mir ist nicht ersichtlich wie ich vorzugehen habe

für jede Hilfe! :)

Answer 1

Das Rechteck mit der Breite t hat die Höhe f(t) und damit die Fläche

A = t·e^(-t)

Damit die Fläche maximal ist, muss die Ableitung Null sein

A' = 1·e^(-t) - t·e^(-t) = (1 - t)·e^(-t) = 0 → t = 1

Answer 2

Hallo

der Flächeninhalt ist doch einfach F(t)=t*f(t)also F=t*e^-t und davon das Max zu finden sollte nicht so schwer sein?

(Kontrolle t=1)

Gruß lul

Comments

Ich verstehe leider gar nichts :x