Flächen- und Höhenberechnung: Logo aus den beiden Funktionen f(x) = e0,5x-1 und g(x) = e0,25-0,75x

Question

Aufgabe:

Betrachtet werden die beiden Funktionen f(x) = e^0,5x-1 und g(x) = e^0,25-0,75x.

Ein Designer entwickeltaus den beiden Funktionen das schematisch dargestellte Logo der Breite 3 cm, wobei der Schnittpunkt der Graphen genau in der Mitte liegt. Welche Höhe und welchen Flächeninhalt hat das Logo?

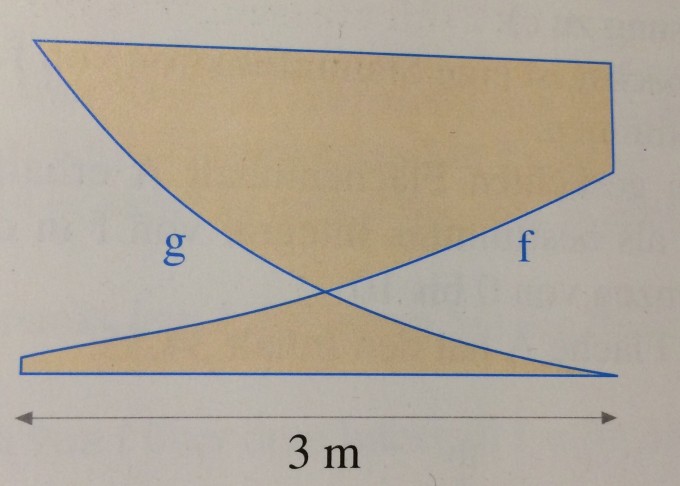
Problem/Ansatz:

Den Schnittpunkt zu berechnen ist ja nicht schwer, aber weiter komme ich auch nicht. Bitte um Hilfe, Ansatz oder Lösungsweg.

Answer 1

Wo liegen denn genau deine Probleme? Vorstellen kannst du dir das doch schon oder nicht wirklich?

Ich komme auf eine Höhe von 1.671 LE und eine Fläche von 3.162 FE.

Ob die Einheit jetzt cm oder m sind ist nicht ganz klar. in der Skizze stehen Meter und in der Aufgabe cm. Das ist ja aber auch nicht so wichtig.

Comments

Danke für die Antwort, wie bist du den auf die Höhe gekommen?

Vorstellen konnte ich mir das nicht, aber dein Schaubild hat mir weitergeholfen.

---

Dir ist schon klar, dass die Höhe des Schaubildes die Höhe meines gezeichneten Rechtecks ist oder? Also brauchst du nur berechnen wie weil die obere Seite von der unteren entfernt ist.

---

Nein, dass war mir nicht klar. Ich verstehe auch gar nicht, wieso das Rechteck nicht auf der X-Achse draufliegt ? Wie hast du rausbekommen, dass die Rechtecksfläche nach oben verschoben ist und wie weit diese nach oben verschoben ist?

---

Dann schau dir mal die Ecken des Rechtecks genau an. Dann sollte dir vielleicht ein Licht aufgehen. Wie würde der Ausschnitt denn aussehen wenn die obere und untere Seite höher oder Tiefer liegen würden. Von mir aus zeichne dir das gerne mal auf.

Answer 2

Hallo Breite 3cm, also vom Schnittpunkt aus 1,5 nach rechts  dort f(xs+1,5) ist dort die Höhe links g(xs-1,5) ist dort die Höhe.

Fläche durch integrale, von xs-1,5 bis xs von dem Rechteck die Fläche von g-f abziehen  von xs bis xs+1,5  f-g vom Rechteck abziehen, aber skizzier dir das doch selbst.?

Gruß lul

Comments

Danke für die Antwort, leider habe ich das nicht ganz Nachvollziehen können.