Bestimmen Sie die Gerade g so, dass die beiden Flächen inhaltsgleich sind.

Question

Aufgabe:

K ist das Schaubild von f mit f(x)= 2sin(x); xer

a) Die Abbildung zeigt ein Dreieck, dessen Spitze S auf K liegt. Für welches S sind Dreiecksinhalt und Inhalt der markierten Fläche gleich?

b) Bestimmen Sie die Gerade g so, dass die beiden Flächen inhaltsgleich sind.

Problem/Ansatz:

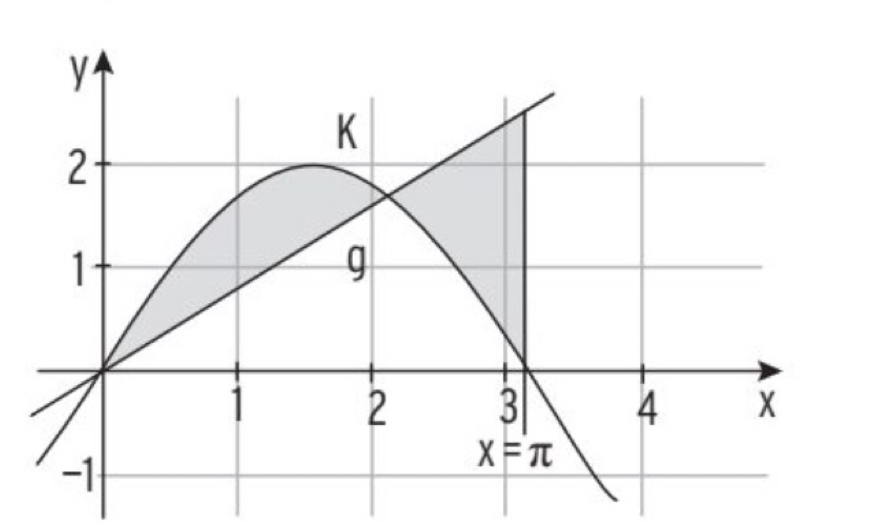
das gehört zu b)

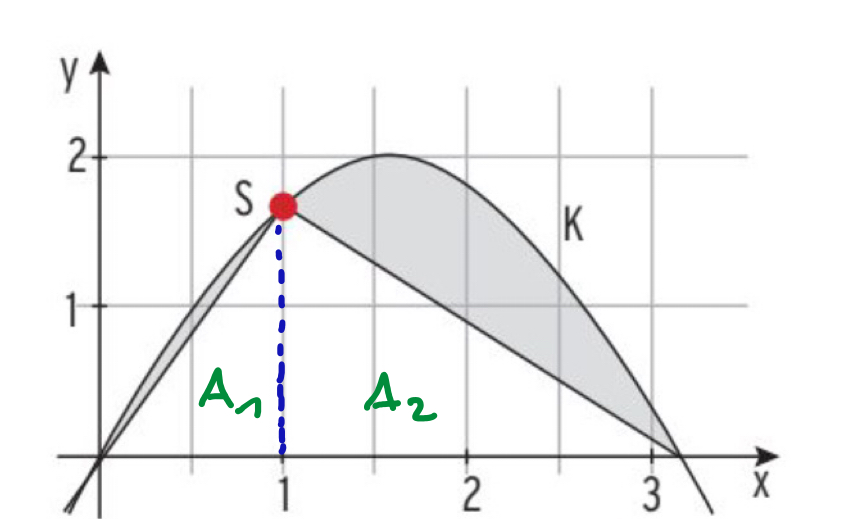
das gehört zu a)

Answer 1

b)

∫ (x = 0 bis pi) (2·SIN(x) - m·x) = 0 --> m = 8/pi^2 = 0.8106

a)

1/2·pi·2·SIN(x) = 2 --> S1(arcsin(2/pi) | 4/pi) ; S1(pi - arcsin(2/pi) | 4/pi)

Comments

Heyy, erstmal danke!!

Aber was ist dieses arc? hab das noch nie gemacht !

Gibt es vielleicht eine einfacheren Lösungsweg?

LG

xxxhelpme

---

arcsin(x) ist sin^{-1}(x) auf dem Taschenrechner. Du kannst das wenn ihr dürft auch numerisch als Dezimalzahl angeben.

---

Ah okay, jetzt passt es danke :)

Eine letzte Frage noch und zwar, warum haben Sie bei b) die Gleichung 0 gesetzt?

---

Wenn die Flächen gleich groß sind dann muss das Integral 0 sein. Du bildest ja die Differenz der Funktionen.

f(x) -g(x) ist positiv wenn f oberhalb von g liegt ansonsten ja negativ.