Gegeben sind zwei Funktionen f(x) und g(x).:
f(x)=3x²-2x+4
g(x)=-x²-2x+8
Berechne den eingeschlossenen Flächeninhalt dieser beiden Funktionen
Erste Frage: Warum gilt für die Fläche F(b)-F(a). Ich verstehe, dass nicht ganz, wenn ich etwa mein Wasserbecken bei y=-4 mit deren Scheitelpunkt (Parabel ansetze) bleibt doch innerhalb der Integralgrenzen a und b noch eine Fläche von der Funktion zur X-Ache Funktion hin besehen. Da sind auch noch Dreiecke außen jeweils links und recht der Parabel (Abschnitte zum Reckteck-sonst was). Nun spielt sich Intervall zwischen meinen Beckenrändern=Nullstellen der Parabel ab. Soll ich jetzt einfach mit F(b)-F(a) drüber integrieren? Woher weiß ich den an dieser Stelle welche Fläche ich berechne.....Die zur X-Achse hin.....ist das bereits die Lösung auf meine Frage?
Zurück zum Beispiel:
1. Schritt:
Ich bestimme die Schnittpunkte der beiden Funktionen (Sie bilden meine Intervallgrenzen und sind glz. meine Nullstellen):
3x²-2x+8=-x²-2x+8
......4x²=4 /:4/wurzel(1)
es folgt: x1=1 und x2=-1
2. Schritt: Ich stelle meine Integralgrenze mit der Formel zur Berechnung von Flächen bei Integralen auf:
$$\int _{ -1 }^{ 1 }{ g(x)- } f(x)dx=$$
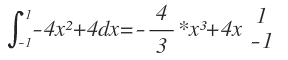
$$(-\frac { 4 }{ 3 } +4)-(\frac { 4 }{ 3 } -4)=\frac { 8 }{ 3 } +\frac { 8 }{ 3 } =16/3$$
Woher sind denn die -4x²+4dx oben
Wenn ich dx berechnen möchte muss ich doch ableiten also so:
Erstes g(x) weil ich die dann mit f(x) subtrahieren werde:
g(x)=-x²-2x+8
g´(x)=-2x-2
g´(1)=-2*1-2=-4....für dx wenn ich 1 für die Grenze b einetze (hingegen würde -1 die +4dx oben vor dem -4/3 ergeben). Ist mein Weg/Gedanke falsch und wenn warum?
Ps: Gibt es eine Alternative zur Berechnung?
mfg