Von zwei Funktionsgraphen eingeschlossenen Flächeninhalt berechnen

Question

Aufgabe:

Berechnen Sie den Inhalt der Fläche, die durch das Schaubild der Funktionen f und g
eingeschlossen wird, mit

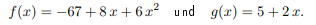
Problem/Ansatz:

Beide Funktionen gleichsetzen, dann die Nullstellen berechnen x1=3; x2=-4

dann integrieren F(x)= 2x^3 + 4x^2 -67x

G(x)= x^2+5x

G(X)-F(X)

dabei komme ich auf ein Ergebnis von A1= 28 und A2= 315

A1-A2= |287|

Ist dies korrekt?

MfG

Comments

also muss ich die 2 Flächeninhalte einfach
addieren und komme so auf mein Ergebnis?

Nein. Subtrahieren.

Eine Funktion ist die " obere Funktion " die
andere die " Funktion darunter ".
Ohne Graph weiß man  zuweilen nicht welche
welche Funktion ist.
Man kann aber immer rechnen
Differenzfunktion = ...
d ( x ) = f ( x ) - g ( x )
Fläche = ∫ d(x) dx zwischen den Schnittpunkten

Sollte als Fläche ein negativer Wert herauskommen dann positiv setzen. Flächen sind immer positiv.

Answer 1

Das kannst du einfacher haben: Differenzfunktion h(x)=g(x)-f(x) bestimmen, Integral der Differenzfunktion in den Grenzen der Nullstellen der Grenzfunktion berechnen. Es kommt 343 heraus. Deine Integrationsgrenzen sind richtig.

Comments

also muss ich die 2 Flächeninhalte einfach addieren und komme so auf mein Ergebnis?

---

Das kommt drauf an, wie du die größere der beiden Flächen berechnet hast. Mach es besser so, wie ich beschrieben habe das ist einfacher und sicherer.