AC habe ich ausgerechnet mit (-3|-1|-3) aber welchen anderen Richtungsvektor nehme ich, um den Winkel zu bekommen?

Question

Aufgabe:

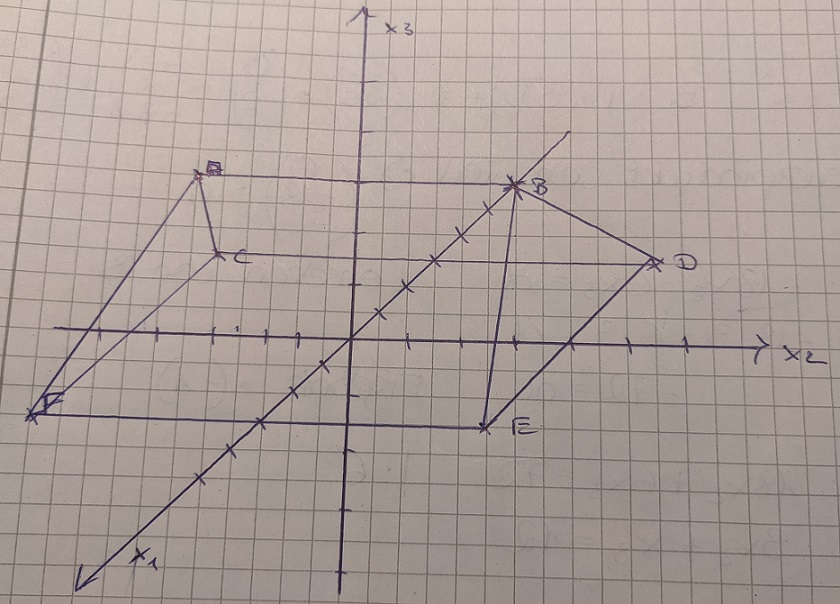
Ein Haus erhält ein Walmdach der Form im Material 1. Die Punkte C, D, E und F sind Eckpunkte des rechteckigen Dachbodens. Das Dach ist symmetrisch zur x1-x3-Ebene. Eine Längeneinheit entspricht einem Meter. Gegeben sind die Punkte A(0|-3|3), C(-3|-4|0), D(-3|4|0) und F(3|-4|0).

- Berechnen Sie den Winkel der Dachkannte AC gegenüber dem Dachboden.

Problem/Ansatz:

B (0|3|3) und E (3|4|0) habe ich bereits berechnet, alle weiteren Aufgaben ebenfalls. Ich verstehe tatsächlich, das mit der Dachkannte AC GEGENÜBER dem Dachboden nicht.

AC habe ich ausgerechnet mit (-3|-1|-3) aber welchen anderen Richtungsvektor nehme ich, um den Winkel zu bekommen?

Answer 1

Den Normalenvektor des Dachbodens [0, 0, 1]

Also

ARCSIN(ABS([-3, -1, -3]·[0, 0, 1])/(ABS([-3, -1, -3])·ABS([0, 0, 1]))) = 43.49°

Man kann es auch über die normale Trigonometrie machen

ARCTAN(3 / √(1^2 + 3^2)) = 43.49°

Comments

Ach und ich habe mir das Hirn zermartert. Dabei ist die Lösung so einfach :D

Lieben Dank für Deine Hilfe!