Flächeninhalt, Dreiecke, Rechteck

Question

Aufgabe:

In einem Rechteck ABCD mit den Seitenlängen
AB =a und BC =b bewegt sich Punkt P von A
nach B mit der Geschwindigkeit 1 cm/s und Punkt Q von B nach C mit der doppelten Geschwindigkeit. P und Q starten zur gleichen Zeit. Wann hat der Flächeninhalt des Dreiecks
BQP die Größe a*b/k erreicht? Wie muss man a, b
und k einrichten, damit die Aufgabe lösbar wird?

Ich hab leider keine Ahnung wie man diese Aufgabe löst, über eine Antwort würde ich mich sehr freuen.

Answer 1

Hallo Sandra,

Willkommen in der Mathelounge!

Ich hab leider keine Ahnung wie man diese Aufgabe löst

Hast Du schon eine Zeichnung gemacht?

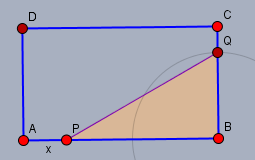
und dann formal aufschreiben, was gegeben ist:$$F_{R} = ab \\ |AP| = x(t) =v t \\ F_{\triangle} = \frac 12 (a-x) 2x = x(a-x)$$Wobei \(F_R\) die Fläche des Rechtecks und \(F_{\triangle}\) die des Dreiecks \(\triangle BQP\) ist. Und jetzt war die Frage:

Wann hat der Flächeninhalt des Dreiecks BQP die Größe a*b/k erreicht?

Setze das mal ein und löse nach \(x\) auf: $$\begin{aligned} F_{\triangle} &= x(a-x) = \frac{ab}k \\ 0 &= x^2 - ax + \frac{ab}k \\ x_{1,2} &= \frac a2 \pm \sqrt{\frac{a^2}4 - \frac{ab}k } \\ &= \frac a2\left( 1 \pm \sqrt{1 - \frac{4b}{ak}} \right)\end{aligned}$$Jetzt noch \(x = t\, \text{m/s}\) einsetzen, wäre zumindest formal eine Antwort, bringt einen aber nicht weiter ...

Wie muss man a, b und k einrichten, damit die Aufgabe lösbar wird?

Es gilt, ein paar Beschrängunken zu berücksichtigen. So muss \(x \le a\) und \(2x \le b\) sein. Weiter sollte der Ausdruck unter der Wurzel positiv oder 0 sein. Also muss gelten:$$a k\ge 4b$$