Exponential Funktion Aufgabe kommen

Question

Aufgabe:

Leute bitte helft mir bei den Aufgaben, bitte schreibt die Rechenschritt auf.

Aufgabe:

Anna und Berta besuchen eine höhere Schule mit 700 Schüler/innen. Aus Langeweile setzen die beiden ein Gerücht in die Welt. Zu Beginn kennen nur 2 Personen (Anna und Berta) das Gerücht. Das Gerücht verbreitet sich aber sehr schnell an der Schule und nach einem Tag kennen bereits 128 Schüler/innen den Inhalt. a) Modellieren Sie die Ausbreitung des Gerüchtes nach dem exponentiellen Wachstum. Ermitteln Sie die Gleichung der Wachstumsfunktion und stellen Sie diese in einem geeigneten Koordinatensystem dar. b) Modellieren Sie die Ausbreitung des Gerüchtes nach dem begrenzten Wachstumsmodell. Ermitteln Sie die Gleichung der Wachstumsfunktion und stellen Sie diese im Koordinatensystem von a) dar. Beachten Sie, dass maximal 700 Schülerinnen an der Schule sind. c) Modellieren Sie die Ausbreitung des Gerüchtes nach dem logistischen Wachstumsmodell. Ermitteln Sie die Gleichung der Wachstumsfunktion und stellen Sie diese im Koordinatensystem a) dar.

Answer 1

(1) Exonentielles Wachstum

Hier ist die Wachstumsfunktion \( f(t) = f(0) e^{\lambda t} \) und \( f(0) = 2 \). Es gilt \( f(1) = 128 \) also \( \lambda = \ln(64) = 4.159 \)

(2) beschränktes Wachstum

Hier ist die Wachstumsfunktion \( g(t) =  G - (G - g(0) ) e^{-\lambda t } \) wobei \( G = 700 \) die obere Schranke darstellt. Aus \( g(1) = 128 \) ergibt sich \( \lambda \)

(3) Logistisches Wachstum

Hier ist die Wachstumsfunktion $$ h(t) = \frac{G}{1+e^{-\alpha G t} \bigg( \frac{G}{h(0)} - 1 \bigg)  } $$ Aus \( h(1)=128 \) bestimmt man wieder \( \alpha \)

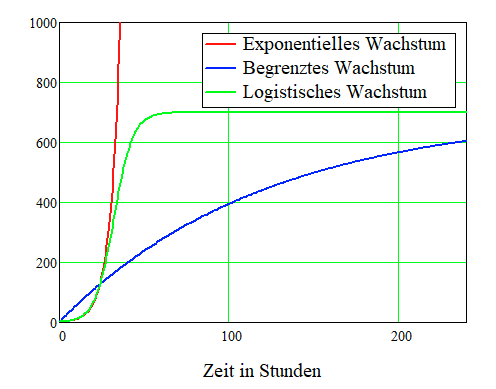
Und es sieht so aus: