Es sei G = (E,K) ein endlicher Graph ohne Schleifen, d.h. jede Kante k ∈ K habe genau zwei verschiedene Elemente. Weiter bezeichne n = |E| die Anzahl der Ecken von G. Für eine Ecke e ∈ E sei der Grad deg(e) von e durch
Institut für Mathematik Prof. Dr. Fabian Januszewski Dr. Tobias Columbus
deg(e) = {k ∈ K | e ∈ k}
(b) Zeigen Sie, dass G eine gerade Anzahl von Ecken hat, falls alle Ecken von G den Grad 5 haben.
(c) Zeigen Sie, dass jeder Graph ohne Schleifen eine gerade Anzahl von Ecken mit ungeradem Grad enthält.
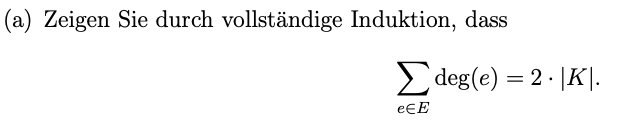
Text erkannt:
(a) Zeigen Sie durch vollständige Induktion, dass
$$ \sum \limits_{e \in E} \operatorname{deg}(e)=2 \cdot|K| $$