Aufgabe:
Erweiterter euklidischer Algorithmus bei ggT(8n + 3, 5n + 2)
Problem/Ansatz:

Text erkannt:
(c) Verwenden Sie den erweiterten euklidischen Algorithmus, um für jeden der folgenden Werte
den \( \operatorname{gg} \mathrm{T}(a, b) \) zu berechnen. Bestimmen Sie außerdem jeweils ganze Zahlen \( x, y \in \mathbb{Z}, \) so dass
\( x a+y b=\operatorname{gg} \mathrm{T}(a, b) \). Geben Sie alle Schritte und Rechnungen an.
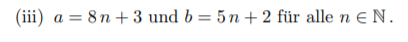
Text erkannt:
(iii) \( a=8 n+3 \) und \( b=5 n+2 \) für alle \( n \in \mathbb{N} \).

Text erkannt:
1117
\( a=8 n+3 \), \( b=5 n+2 \) fur alle \( \omega \in N \)
Also:
Hallo, ich hoffe man kann meine Rechnung einigermaßen erkennen.
Wie ihr sehen könnt, habe ich ich diese Rechnung soweit abgeschlossen, doch wenn ich nun -5*8n+3+8*5n+2 mit einer beliebigen natürlichen Zahl anstelle von n ersetze und ausrechne, kommt 5 anstelle der 1 raus.
Kann mir jemand zufällig einen Tipp geben, wo der Fehler liegt?
Mfg. Jannik