Wie lang ist die Seitenlänge der Fünfecke eines Dodekaeders bei n13 Würfelgröße

Question

Aufgabe:

Wie lang ist die Seitenlänge der Fünfecke eines Dodekaeders ,wenn ich einen 13 cm Würfel habe.

Bin Steinmetz und möchte einen Marmordodekaeder fertigen---vielen Dank Markus

Problem/Ansatz:

Answer 1

Hallo,

schau mal hier nach ,https://de.wikipedia.org/wiki/Dodekaeder#cite_note-1

die Lösung liegt wahrscheinlich beim Innenkugelradiuses.   ca 11,6696cm ohne Gewähr

Comments

Wenn auf einer Würfelfläche eine Dodekaederkante list ist es der Kantenkugelradius

wenn auf einer Würfelfläche eine Fünfeckfläche liegt ist es der Umkugelradius.

Um das Mamordodekaeder zu bauen, würde ich erstes bevorzugen, dh das die Kante auf der Würfelfläche liegt,

diese Kante ist Würfelkante / (Goldener Schnitt zum Quadrat) und ich habe es letzten Wochen zufällig mit Vollholz gemacht, und nach der Erklärung von Euklid mit den Dächern auf einen Würfel gezeichnet und mit einer Winkeleinstellung auf Kapp oder Bandsäge geschnitten.

---

Viel Erfolg dabei, vielleicht findest du auch anregungen bei MC Escher!

Answer 2

Das wird schwierig - ich nehme an, dass Du berufsbedingt von einem Würfel alles weghauen willst was nicht zu einem Dodekaeder gehört?

Dass man ein Dodekaeder dagegen nicht in einen Würfel einbeschreiben kann, lässt sich folgendermaßen begründen: Ein Dodekaeder hat 20 Ecken, ein Würfel hat 6 Seitenflächen. Auf jeder Seitenfläche des Würfels müssen im Durchschnitt also mehr als 3 Dodekaederecken liegen. 3 Ecken definieren aber eine Fläche. Wenn also 3 Dodekaederecken auf einer Würfelseitenfläche liegen, dann müssen zwangsläufig alle 5 Ecken einer Dodekaederseitenfläche auf dieser Würfelseitenfläche liegen. Es muss aber mindestens noch eine weitere Würfelseitenfläche mit 5 Dodekaederecken geben. Dies kann nur die gegenüberliegende Seitenfläche sein. Von den 20 Dodekaederecken bleiben dann noch 10 Ecken übrig. Wenn man von oben auf ein auf einer Seitenfläche liegendes Dodekaeder schaut, dann bilden diese 10 Ecken als Projektion ein regelmäßiges Zehneck. Die Ecken dieses Zehnecks müssten dann auf der Projektion der übrigen 4 Seitenflächen des Würfels, einem Quadrat, liegen. Das ist aber unmöglich, weil dann auch 3 Ecken auf einer Seite des Quadrats liegen müssten

entnommen aus.

http://www.brefeld.homepage.t-online.de/wuerfel-einbeschrieben.html

Ich hänge mal das Ergebnis meiner Bastelstunde an. Wenn ich einen Würfel über die äußeren Kanten (der Walmdachgiebel der Walmdachansätze des Innenwürfels)  lege, dann käme man auf

Dann muß aber relativ viel weg. Ob das auch mit einem geringeren Materialabtrag geht hab nicht hinterfragt...

Answer 3

$$k=13*sin(36)/(2*sin(54))≈4,723cm$$

Die Kantenlänge des Dodekaeders beträgt etwa 4,7 cm.

Begründung, ich habe dieobere ind Interesse Fläche des Dodekaedes parallel zur oberen und unteren Fläche des Wüefels ausgerichtet. Wenn ich die jeweils übernächsten Eckpumkte eine Fünfecks der Kantenlänge k verbinde, dann hat diese Strecke die Länge

b=2*k*sin (54°)

Der Außenradius des Fünfecks mit der Kantenlänge b beträgt

r=k*sin(54°)/sin(36°) dieser Dodekaeder muss nun also in den Würfel mit der Kantenlänge 13 cm passen.

$$13=2r =k*2*sin(54°)/sin(35°)$$

Dies führt zur obigen Formel.

Der Dodekaeder von Wächter scheint aber größer zu werden..

Comments

Wenn ich eine Dodekaederfläche auf eine Würfelseite lege (war das so gemeint - ohne Autokorrektur;-) dann komm ich auf Dein Ergebnis muss allerdings noch mehr Material abtragen

Das bedeutet ca 63% muss weg und es wird wohl schwieriger werden die Schnittflächen auszurechnen. In meiner oben vorgestellten Anordnung muss bereits ca. 57% Material abgenommen werden...

---

Ja, genau das habe ich erwartet. Nun könnten wir noch den Mittelpunkt vom Dodekaeders auf den Mittelpunktpunkt  des Würfels legen und dann hätten wir ja oben und unten noch Luft . Durch Drehungen könnten wir an allen Punkten Luft verschaffen , die wir nutzen könnten um den Dodekaeder zu vergrößern . Dann kommen wir auf deine Lösung. Deine Lösung ist die größtmöglichste, denn dann können wir den Dodekaeder in keine Richtung mehr drehen.

Answer 4

Hallo Salamander

Wie schon zwei Lösungen vorgestellt wurden, bei sind dafür geeignet, ich bevorzuge die wie sie wächter schon beschreibt, und ich mache seit einigen Wochen auf diese Basis Dodecaeder aus Vollholz mit der Kapp und/oder Bandsäge und stelle ansich nur einen Winkel ein, um damit alle Fünfecke zu erhalten.

Text erkannt:

\( F \)

Das mit Dächern beschrieb auch Euklid in seinem Buch vor 2300 Jahre, dh 6 Dächer (Gibel ist Kante von Rechteck bzw. Seiten von zwei Fünfecke) platzieren und alles wo die Dächer nach aussen übersteht abschneidern (bei Vollholz bzw. Mamorwürfel schneiden man ansich nach drehen den Überstand automatisch weg) sind die Fünfecke fertig. den Schnittwinkel kann man auch konstruieren, von der Kante einer schon eingezeichnetenn Fünfeckseite zum Ende der nächsten Fünfeck Kante. (Rote Linie ist der Schnitt, und das auf jeder Würfelfläche von Grün-Rot Linie zur ende der Grünen Linie, auch auf der jeweils gegenüberliegenden Würfelfläche)

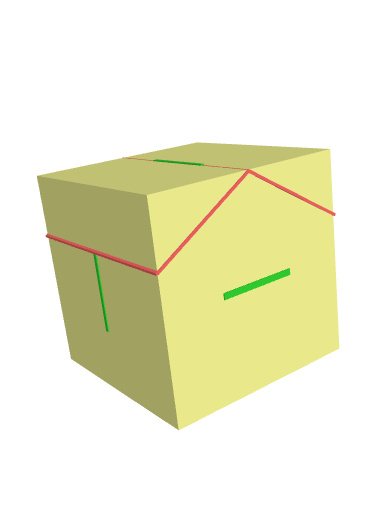
Wie Seitenkante von Fünfeck in der Fläche des Würfels zustande kommt, vorstellen kann man sich so, das man 3 Rechtecke im Rechten Winkel zueinandersetzt (siehe meine Grafik) damit hat man die ersten 6 Dodecaeder Kanten, diese Rechtecke sind Goldene Rechtecke zum Quadrat dh zb Würfelkante / (Goldener Schnitt (1,618...) zum Quadrat).

also 13 / (1,618*1,618) = 4,9565766768

oder Würfelkante / 1,309

der Winkel einer sogenannten Dachfläche ist 31.7 Grad (wenn man es ausrechnet)

setzt man dann noch einen Würfel der Im Goldenen Verhältnis zum Aussenwürfel zentriert ist, erhält man auch die restlichen Ecken aller Fünfecke, und wenn man jetzt jeden Eckpunkt mit den näheren 3 Eckpunkte verbindet ist das Dodekaeder fertig.

Wäre neugierig auf ein Foto vom Mamor Dodecaeder

anbei noch mein Vollholz Dodekaeder, geschnitten mit dem Prinzip der Dächer nach Euklid. dh einmal auf der Bandsäge eine Winkelanschlag von 31,7 gemacht und damit alle Ecken geschnitten.

gruss franz