Mittlerweile ist Abend, doch gut Ding will Weile haben.
Skizze von Werner - Salomon
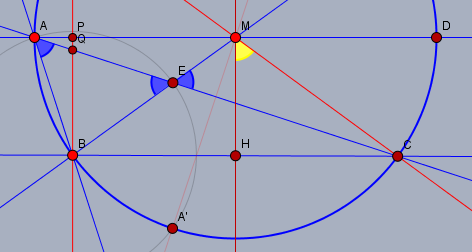
Laut Aufgabe:
$$ε=∠ BAC=∠BAE= ∠AEB$$Der Zentriwinkel ist doppelt so groß wie der Peripheriewinkel.$$∠BMC=2*∠BAC=2ε$$Der gestreckte Winkel$$∠AMD=180°$$Das Lot in M halbiert den gestreckten Winkel, aufgrund der Symmetrie aber auch den erwähnten Zentriwinkel.$$∠AMH=∠HMD=180/2=90°$$$$∠BMH=∠HMC=2ε/2=ε$$Damit ist $$∠CMD=∠HMD-∠HMC$$$$∠CMD=90 - ε$$Wir erinnern uns an:
Der Zentriwinkel ist doppelt so groß wie der Peripheriewinkel.$$∠CMD=2*∠CAD$$$$∠CAD=∠CMD/2$$$$∠CAD=(90-ε)/2=45 - 0,5 ε$$damit$$∠BAD= ∠BAC+ ∠CAD$$$$∠BAD=ε+45 - 0,5 ε=45 + 0,5 ε$$Wechselwinkel sind gleich$$∠MBP= ∠BMH = ε$$Winkelsumme im Dreieck=180°$$∠ EBA+∠BAE +∠AEB=180°$$$$∠ EBA=180 -∠BAE +∠AEB$$$$∠ EBA=180-2ε$$Damit$$∠ PBA=∠ EBA-∠ EBP$$$$∠ PBA=180-2ε-ε$$$$∠ PBA=180-3ε$$Jetzt wieder Winkelsumme im ΔPBA$$∠ PBA+∠ BAP+∠APB=180$$$$(180-3ε)+(45+0,5ε)+90=180$$$$2,5ε=135$$$$ε=135/2,5$$$$ε=54°$$
Fertig, der Rest ist für die Chronik.
Guten Morgen,
Leider sind die Bilder nicht zu sehen.
Ich mache die Bilder mit meinem Smartphone.
Gruß, Hogar
Im linken rechtwinkligen Dreieck mit der Kathete A
(45-0,5ε+ε )+(180-3ε)=90
135=2,5ε
ε=54°
0,5(90-ε) = 45-0,5ε
Zentriwinkel<>Peripheriewinkel (über D)
180 -3ε=(180-2ε)-ε
Winkelsumme -2ε - Wechselwinkel ε