Rotationen im Geoknecht3D (Teil 2 von 2)
Im ersten Teil hatte ich beschrieben, wie man aus der Position eines Quaders oder Zylinder sowie den Drehwinkeln die zugehörige Transformationsmatrix aufstellt. Hier kommt nun der umgekehrte Weg.
Die inverse Kinematik
Jetzt wissen wir zwar wie man die Transformationsmatrix für gegebene Winkel \(\alpha\), \(\beta\) und \(\gamma\) berechnet, aber das ist ja gar nicht das Problem. Es ist doch eher so, dass man einen Körper (Quader oder Zylinder) an eine bestimmte Position in eine bestimmte Lage bringen will.
Beispielsweise in dieser Aufgabe, wo u.a. der Abstand der Spitze einer Pyramide von deren Grundfkäche berechnet werden sollte. So eine quadratische Pyramide lässt sich einfach mit dem zylinder-Kommando im Geoknecht3D darstellen.
zylinder(3.5|2.5|2 5|0|3.536|4)
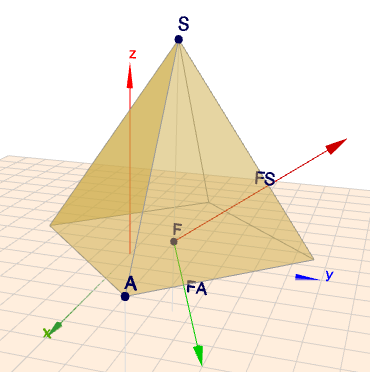
Die Position \(p\) der Pyramide (Zylinder) ist der Punkt \(F\) und die \(3.536\) sind das \(|FA| = 5/\sqrt 2\). Mit dem Parameter \(s=4\) am Ende hat der 'Zylinder' nur 4 Seiten und wird somit zur quadratischen Pyramide. Nur diese Pyramide soll schräg im Raum schweben; und zwar derart, dass sich der Punkt \(A\) an der Spitze des grünen und der Punkt \(S\) an der Spitze des roten Vektors liegen! Im Grunde reicht eine Drehung um X mit -45° und anschließende Drehung um das lokale Z mit 45°. Aber das wäre die Reihenfolge x-z!?
Die passende Transformationsmatrix ließe sich relativ leicht aufstellen, da die Eckpunkte der Pyramide alle gegeben sind. Sei \(n\) der Vektor in die lokale X-Richtung, \(o\) die lokale Y-Richtung und \(a\) die lokale Z-Richtung, so ist$$n = \frac{\vec {FA}}{|FA|}, \quad a = \frac{\vec FS}{|FS|}, \quad o = a \times n$$Werfen wir einen Blick in die Rotationsmatrix $$\begin{aligned} R_{yzx} &= \begin{pmatrix} n_x& o_x& a_x\\ n_y& o_y& a_y\\ n_z& o_z& a_z\end{pmatrix}\\ &= \begin{pmatrix} \text c_\beta \text c_\gamma & -\text c_\alpha \text c_\beta \text s_\gamma + \text s_\alpha \text s_\beta& \text s_\alpha\text c_\beta \text s_\gamma + \text c_\alpha \text s_\beta\\ \text s_\gamma & \text c_\alpha\text c_\gamma& -\text s_\alpha \text c_\gamma\\ -\text s_\beta \text c_\gamma& \text c_\alpha \text s_\beta \text s_\gamma + \text s_\alpha \text c_\beta& -\text s_\alpha \text s_\beta \text s_\gamma + \text c_\alpha \text c_\beta \end{pmatrix} \end{aligned}$$ Ich betrachte zunächst den allgemeinen Fall, für den \(|s_\gamma| \ne 1\) ist. Zusätzlich muss man am Anfang das Vorzeichen von \(c_\gamma\) raten! Nehmen wir also im ersten Schritt an, dass \(c_\gamma \gt 0\) ist. In der Matrix finden wir die Elemente $$n_x = \text c_\beta \text c_\gamma, \quad n_z= -\text s_\beta \text c_\gamma$$Daraus folgt:$$ \beta = \arctan2(n_x, -n_z)$$Ich verwende hier den Arkustangens2, da diese Funktion im Intervall \((-\pi; +\pi]\) eindeutig ist; im Gegensatz zum \(\arctan\). Gleiches gilt für \(\alpha\):$$\alpha = \arctan2(o_y, - a_y)$$Und sind \(\alpha\) und \(\beta\) bekannt, so ist$$\gamma = \arctan2\left( \frac{n_x}{c_\beta}, n_y \right)$$Mit diesen (vorläufigen) drei Winkeln berechnet man wieder rückwärts(!) die Elemente \(o_x\) und \(o_z\). Falls die Ergebnisse dann nicht mit den gegebenen Werten überein stimmen, nimmt man an, dass \(c_\gamma \lt 0\) ist. Dazu ändert man die Winkel \(\alpha\) und \(\beta\) um \(180°\) und berechnet \(\gamma\) neu.
Für den Fall \(|s_y|=1\) ist \(c_\gamma=0\) und folglich sind \(n_x,\), \(n_z\), \(o_y\) und \(a_y\) jeweils \(=0\). Das bedeutet, dass \(|\gamma|=90°\) sein muss. Dadurch wird die Drehachse für \(\alpha\) auf die von \(\beta\) gedreht. Somit spielt für diesen Zustand nur die Summe \(\alpha + \beta\) eine Rolle, und es ist irrelevant, wie groß die einzelnen Winkel sind. Wir können also dann getrost \(\beta=0\) setzen und \(\alpha\) berechnet sich aus$$\alpha = \arctan2\left( -o_x, a_x\right), \quad \text{für}\space |\gamma| = 90°$$
Bleibt noch die Position \(p'\) für Geoknecht3D. Aus der Transformationsmatrix \(T\) folgt:$$\begin{aligned} p= p' + d - R_{yzx} d \\ \implies p' = p - d + R_{yzx} d\end{aligned}$$und so können wir die Position \(p'\) berechnen, die in den Zylinder-Kommando einzutragen ist. Zur Veranschaulichung tue ich dies für das oben erwähnte Beispiel
zylinder(3.5|4.5|1 5|0|3.536|4){ca4}[-62.06|38.66|25.10]
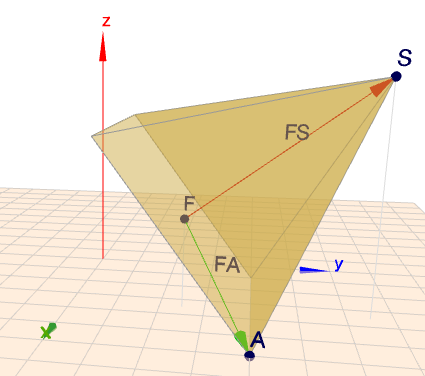
Jetzt bin ich nur noch gespannt, wann ich die erste Geoknecht3D-Szene in der Mathelounge sehe, die den hier beschriebenen Algorithmus ausnutzt.
Viel Spaß damit, und immer schön auf die Bilder klicken ;-)