Gleichung von einer Geraden durch P(-2/1) und Q(5/0) bestimmen

Question

Ich habe 2 Punkte (P/Q)

P: (-2/1) Q: (5/0)

Wie kann ich daraus eine Gleichung erstellen?

Ist damit gemeint ein Term für P und Q?

Answer 1

 

wenn Du 2 Punkte gegeben hast, kannst Du damit leicht eine Funktions- bzw. Geradengleichung erstellen:

P(-2|1), Q(5|0) sind gegeben.

Die Steigung m der Geraden ist damit (0-1)/[(5 - (-2)] = -1/7

 

Die allgemeine Form einer Geraden lautet

y = mx + b

Das m haben wir schon, setzen wir also den Punkt P in diese Gleichung ein:

1 = -1/7 * (-2) + b

1 = 2/7 + b

b = 1 - 2/7 = 7/7 - 2/7 = 5/7

 

Damit hat die Gerade die Funktionsgleichung

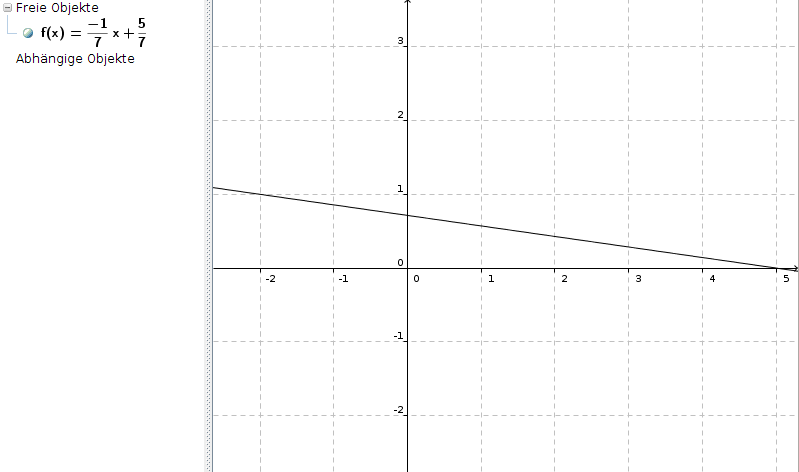
f(x) = y = -1/7 * x + 5/7

 

So sieht sie aus (Du siehst, dass P und Q auf dieser Geraden liegen):

Besten Gruß

 

P.S. "Term", nicht "Therm" :-D

Comments

Du bist immmmre schneelller als ich :(
Aber sehr gute Antwort! :)

---

@Brucybabe: Lass dir nächstes mal bei einer Frage bisschen mehr Zeit (damit ich auch eine Frage beantworten kann) :P Bist immer so ganz schnell :D

---

@Emre:

Ich kenne das Problem: Unknown und der Mathecoach sind im Allgemeinen schneller als der Schall :-)

---

Hahaha ja, aber du auch. Ich frag mich immer und immer wie die das machen?? :)

---

Üben, üben, üben - und immer nur die Fragen beantworten, zu denen ich einen gewissen Zugang habe :-D

---

Da hast du mal wieder Recht! :D Übung macht den Meister :D

Answer 2

Es gibt eine "Formel", die Zweipunkteform einer Geraden, die man hier nutzen kann. Sie lautet allgemein:

$$y={ y }_{ 1 }+\frac { y_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } (x-{ x }_{ 1 })$$

Hierin sind x₁ bzw. y₁ die x - bzw. y - Koordinaten des einen Punktes und  x₂ bzw. y₂ die x - bzw. y - Koordinaten des anderen Punktes. Setzt man die Koordinaten der gegebenen Punkte P und Q entsprechend in die Zweipunkteform ein, so erhält man:

$$y={ 1 }+\frac { 0-{ 1 } }{ 5-(-2) } (x-(-2))$$Nun noch ausrechnen:$$\Leftrightarrow y=1-\frac { 1 }{ 7 } (x+2)$$$$\Leftrightarrow y=1-\frac { 1 }{ 7 } x-\frac { 2 }{ 7 }$$$$\Leftrightarrow y=-\frac { 1 }{ 7 } x+\frac { 5 }{ 7 }$$