Aufgabe:
Text erkannt:
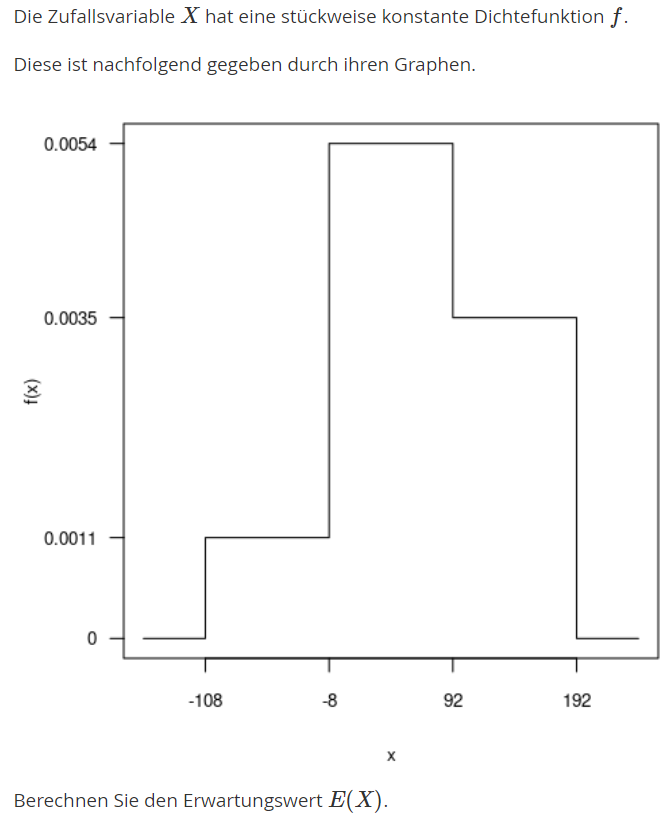
Die Zufallsvariable \( X \) hat eine stückweise konstante Dichtefunktion \( f \).
Diese ist nachfolgend gegeben durch ihren Graphen.
\( x \)
Berechnen Sie den Erwartungswert \( E(X) \)
Problem/Ansatz: Hallo, kann mir jemand bitte helfen? Habe so gerechnet: 0,0011*(-108-(-8) / 2 = -0,055
0,0054*(92-(-8) / 2 = 0,25
0,0035*(192-92) / 2 = 0,175
Was mich zum Ergebnis 0,37 führt, jedoch ist das falsch... wo liegt mein Fehler?
LG