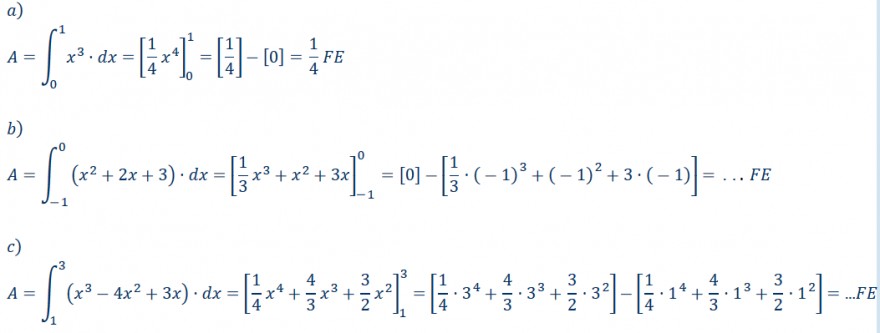
Text erkannt:
a) \( A=\int \limits_{0}^{1} x^{3} \cdot d x=\left[\frac{1}{4} x^{4}\right]_{0}^{1}=\left[\frac{1}{4}\right]-[0]=\frac{1}{4} F E \)
b) \( A=\int \limits_{-1}^{0}\left(x^{2}+2 x+3\right) \cdot d x=\left[\frac{1}{3} x^{3}+x^{2}+3 x\right]_{-1}^{0}=[0]-\left[\frac{1}{3} \cdot(-1)^{3}+(-1)^{2}+3 \cdot(-1)\right]=\ldots F E \)
c) \( A=\int \limits_{1}^{3}\left(x^{3}-4 x^{2}+3 x\right) \cdot d x=\left[\frac{1}{4} x^{4}+\frac{4}{3} x^{3}+\frac{3}{2} x^{2}\right]_{1}^{3}=\left[\frac{1}{4} \cdot 3^{4}+\frac{4}{3} \cdot 3^{3}+\frac{3}{2} \cdot 3^{2}\right]-\left[\frac{1}{4} \cdot 1^{4}+\frac{4}{3} \cdot 1^{3}+\frac{3}{2} \cdot 1^{2}\right]=\ldots F E \)